Физичните закони и Божественият ред
„Случаят владее света“
Теофраст
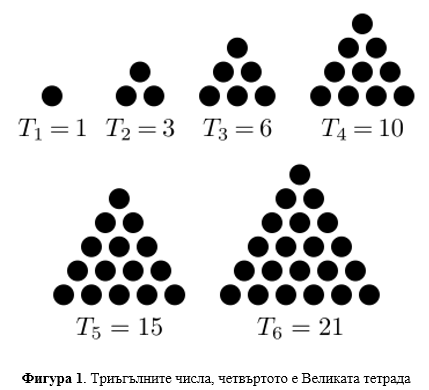
Теофраст е наследникът на Аристотел в перипатетическата школа, авторът на „Характери“ и на много научни и философски изследвания като “Historia Plantarum”, с което се превръща в баща на ботаниката, но и други в биологията, физиката, етиката и метафизиката. Цитираната от него фраза в (Bogdanov, 2016) е довела до обвинения в безбожие. От днешна гледна точка е трудно да се разбере защо това вероятностно наблюдение би могло да бъде сметнато като обидно, тъй като сме израсли в свят, за който се знае (от специалистите), че случайността има огромна роля във физиката, в природата и в успеха и провала на всеки човек (Taleb 2009, Mlodinow 2011). Ние разделяме физичните закони и тяхната природа от представата ни за Бога, но за гръцките учени и философи такова разделение не е съществувало. Питагорейската философска школа търси Божественото проявление сред математическите закони, подобни на тези на свещената тетрада (Фиг.1) – триъгълно число, получено чрез сбора на първите четири естествени числа. Всяко поредно триъгълно число е предишното число, с добавено поредното естествено число, или сумата на естествените числа до неговия номер – четвъртото е сумата на 1, 2, 3 и 4.
Редовете на тетрадата са основата и на музикалната теория на Питагорейците – съотношенията 4:3 (кварта), 3:2 и 2:1 (октава) са основните интервали на Питагорейската скала. Подобни целочислени пропорции питагорейците наблюдавали и сред видимото движение на Слънцето и планетите около Земята, което те нарекли „музиката на небесните сфери“. Тези и други зависимости от теория на числата, лежащи в основата на музиката, астрономията и математиката, те наследили от Вавилон (Van der Waerden 1968) и доразвили в стройна и логически съвършена теория на пропорциите, намерила своето място като книга VII на „Елементи“ на Евклид. Преходът от вавилонска към гръцка математика се състои в изграждането на непротиворечиви логически системи и строгото доказване на всяко твърдение – родоначалникът тук е Талес от Милет, един от седемте мъдреци. Съчетанието на религиозното учение с науката на питагорейците не е така мистично, както е възприето от нашите съвременници, които не са въведени в дълбоката красота на истините от теорията на числата и мистичното чувство, което те внушават. По думите на принца на математиката – “princeps mathematicorum” Гаус „всеки, който се отдаде на аритметиката, развива нещо като страст към нея“ (Dunnington 2004: 413). Гаус приема единствено теория на числата като априорна истина, а геометрията е следствие на пространствената интуиция, отражение на реалния свят (Mackay, 1991: 100):
„Длъжни сме да признаем със смирение, че докато числата са изцяло продукт на нашите умове, пространството притежава реалност извън нашите умове, затова ние не можем напълно да припишем неговите свойства a priori.“
Подобно е отношението на първите истински математици, специалистите по теория на числата сред школата на математиците, наследници на Питагор с една малка разлика – числата са не просто плод на нашите умове, а на Разума, на който те са отражение.
Божественото при тях и по – късно при Платон е пряко свързано с с регулярността, която се наблюдава в Космоса – кръговите орбити на планетите, движени от точни, математически закони са проява на един естествен ред. Удивително е било за древните философи наличието на порядък в Космоса. Удивително е и днес при целия напредък на науката, че такъв ред изобщо съществува, че законите на физиката са постоянни във времето и пространството, че има физични константи, че скоростта на светлината във времето и пространството е една и съща във вакуум. Това удивление по особен начин изразява Юджийн Уигнър в прословутата си статия „Необяснимата ефективност на математиката в природните науки“, преведена на български в сборното издание „Проблеми на съвременната математика“ (Wigner 1973: 98):
„Светът около нас е объркващо сложен и най-очебийният факт за него е, че можем да предвиждаме бъдещето. Макар известната шега да приписва на оптимиста възгледа, че бъдещето е несигурно, в този случай оптимистът е прав: бъдещето е непредсказуемо. Както отбелязва Шрьодингер, цяло чудо е, че въпреки загадъчната сложност на света в явленията могат да се открият известни закономерности. Една такава закономерност, открита от Галилей, е, че два камъка, пуснати по едно и също време от една и съща височина, стигат до Земята за едно и също време. Законите на природата са свързани с такива закономерности. Закономерността на Галилей е прообраз на широк клас закономерности. Тя е изненадваща закономерност поради три причини.
Първата причина за нейната неочакваност е, че е вярна не само в Пиза, но и по времето на Галилей, но че е вярна навсякъде по Земята, била е винаги вярна и пак ще бъде вярна. Това свойство на закономерността е осъзнато инвариантно свойство и преди известно време аз имах възможност да посоча, че без принципи на инвариантност, подобни на този, който следва от това обобщение на наблюдението на Галилей, не би била възможна никаква физика. Втората неочаквана особеност е, че разглежданата закономерност не зависи от толкова многото условия, които биха могли да влияят върху нея. Тя е в сила независимо от това, дали вали или не, дали опитът се провежда в стая, или от наклонената кула, независимо от това дали лицето, което пуска камъка е мъж или жена… Очевидно има безброй други условия, които са несъществени от гледна точка на валидността на закона на Галилей. Неподатливостта на толкова много обстоятелства, които биха могли да играят роля в наблюдаваното явление също е наричана инвариантност…. И тъй, вярно е твърдението, че ако нямаше явления, които да са независими от всички освен от едно управляемо малко множество от условия, физиката би била невъзможна.
… Предишното разглеждане има за цел на първо място да припомни, че съществуването на „природни закони“ съвсем не е естествено, а още по-малко естествена е възможността човек да може да ги открива (Е. Шрьодингер в книгата си What is Life, Camebridge, 1945, стр.31 пише, че това второ чудо може би надхвърля човешките възможности за разбиране)“
Това, което удивлява Уигнър и Шрьодингер се състои от два основни компонента. Първият е, че физическите закони са математически, т.е. изобщо, че има закони, неподвластни на времето и пространството, удивително от вероятностна гледна точка. Второто е, че изобщо е възможно те да бъдат открити зад безкрайното количество взаимодействия и влияния, които могат да попречат на това откритие и ефективно правят вероятността в общия случай да се открие закон да е с мярка 0. Малкото управляемо множество от условия е безкрайно малко, сравнено с безкрайното множество, от което едно явление може да зависи. Това учудване от познаваемостта на Природата не е съвременно, обаче – то датира от времето на зараждането на научния метод в Древна Елада. Питагорейците наследили много удивителни математически закони от Вавилон, но още по-удивително е, че създадената от тях теория на музиката, базирана на теория на числата била потвърдена по-късно чрез експериментиране върху монохордата, както и движението на небесните сфери, съвпадащо удивително с основаните на целочислени пропорции закони. За тях самите числа били пораждащи за всичко във Вселената – възглед, удивително близък до този на Гаус за априорните истини. Обожествяването на числата намерило израз и в тяхната клетва (Van der Waerden, 1968):
“Аз се кълна в оня, който повери на нашата душа тетрадата, в която лежи изворът и коренът на вечната природа“
Астрономичният модел на Питагорейския философ Филола отхвърля Земята като център на Слънчевата система, според него Земята, Слънцето и другите тела се движат около един център – небесен огън – най-близката до реалността концепция (Слънцето и планетите се въртят около барицентъра на Слънчевата система). Този космически ред, който те съзрели, трябвало да има своя първоизточник – Бог. Божественото и физичните закони за тях и по-късно за Платон били едно и също. Това е същият възглед като този на Алберт Айнщайн, който казва (Einstein, 2013):
„Научното изследване е основано на идеята, че всичко, което се случва е определено от законите на природата и следоавателно това важи за действията на хората. Поради тази причина, един учен изследовател едва ли ще бъде склонен да вярва, че събитията могат да бъдат повлияни от молитва, т.е. от желание адресирано до свръхестествено същество. Все пак трябва да се признае, че нашето истинско знание на тези закони е само несъвършено и непълно, така, че всъщност убеждението в съществуването на базови, универсално валидни закони в природата също почива на вид вяра. По същото време тази вяра е като цяло оправдана досега от успеха на научните изследвания. Но, от друга страна, всеки, който е сериозно въвлечен в развитието на науката се убеждава, че един дух се проявява в законите на вселената – един дух, много по-превъзхождащ човешкия и в чието лице ние с нашите скромни сили трябва да се чувстваме смирени. По този начин развитието на науката води до религиозно чувство от специален вид, който е наистина твърде различен от религиозността на някой по-наивен“
Това виждане е твърде близко до питагорейското. По думите на (Van der Waerden, 1968):
„Представителите на тази школа винаги са се придържали към мнението, че небесните светила са божествени, одушевени, живи същества, които вследствие на своята вечна божествена природа вечно еднакво описват съвършени кръгови движения. Светилата с разума опознават закона на своето движение и се движат съзнаелно, точно както нравствният човек не позволява на изменчивите страсти да властвуват над него, а живее съобразно изискванията на разума.“
Вярванията на питагорейците не бива да се тълкуват изолирано от контекста на факта, че тяхната школа развива систематичния научен метод и строгото логическо доказателство в областта на аритметиката, като наследници на първопроходеца Талес от Милет. Това, което те виждат е отлика между движението на планетите и случайността, по същия начин, по който човешкото поведение се подчинява на закони и хората действуват целенасочено, а не случайно. Целенасочеността е проявление на разума, а закономерността е проявление на целенасочеността. Оттам те заключават, че регулярното движение на планетите е целенасочено и оттам – продукт на разум. Това не е твърде далече от Аристотел и неговата визия за Бог като първопричина за движението в света – защото движението не е случайно, а целенасочено и следователно има своя източник, който е активният интелект – онова, което задвижва всичко, без само да се движи (Aristotle [350 BCE.], 2000: 60):
„Но умът действа, когато го притежава: така че божественото, което умът явно има, е по-скоро действителността на това притежание, отколкото възможността за него, и размисълът е най-приятното и най-доброто. Това, че богът притежава винаги доброто състояние, в което ние се намираме само понякога, е чудесно: но пък ако неговото състояние е още по-хубаво, това би било още по-необикновено. Но е точно така. И животът също е в него: защото действителността на ума е живот, богът е действителност, а действието само благодарение на себе си е неговият живот, който е прекрасен и вечен. Казваме, че богът е живо същество, което е добро във висша степен и е вечно, така че животът и непрекъснатата и вечна непреходност принадлежат на бога – нали това е богът. “
Вярата в Бог в древна Елада (при Питагорейците, Платон и Аристотел) е вяра в първенството на Разума. Корените на това са в развитието на математиката на строга логическа основа. Диалектиката на Платон се гради на доказателството със свеждане до противоречие reductio ad absurdum, използвано, за да докаже, че диагоналът на квадрата е несъизмерим със страната му – ирационално количество (корен от две). Самият Платон стига дотам, да заяви (Germain, 1912: 211):
„Недостоен е да се смята за човек онзи, който не знае, че диагоналът на квадрата е несъизмерим със страната му“
Разумът е това, което определя човека, а това знание е в основата на метода за търсене на истината според Платон, следователно то е есенциално за всеки, който се смята за човек. Този логически подход се пренася и върху теологията, както илюстрира и цитатът от Аристотеловата Метафизика. Това обединение на теология и наука е причината за своеобразния начин на мислене на атеистите в Древна Елада – за да отхвърлят Божественото, те отхвърлят и научното; за да приемат планетите за просто небесни тела, а не разумни същества, те търсят случайното.
Атеизмът в древна Елада и случайното
Анаксагор от Клазомена
Анаксагор е натурфилософ, ползващ се с голямо уважение в Атина. Негов ученик бил Перикъл – неговите политически противници обвинили Анаксагор в безбожие, тъй като учил, че Слънцето и звездите били мъртви нажежени камъни. Анаксагор бил осъден и изгонен от Атина. Част от неговите заслуги като астроном са свързании с това, че учил, че Луната получава своята светлина от Слънцето и дал правилно обяснение за слънчевите и лунни затъмнения (Van der Waerden 1968: 179). Той дал по – добра оценка за големината на Слънцето – то било по-голямо от Пелопонес.
Въпреки своите заслуги, влиянието на Анаксагор върху астрономията като цяло не е било благоприятно. Причината е, че той си представял небесните тела като мъртви неодушевени предмети, които се движат не по математически закони, а се увличат от вихровото движение на ефира. Слънцето и Луната се увличат от вихровото движение по-бавно, отколкото неподвижните звезди и поради това изостават от тях. Това породило друг проблем – как се получава, че Слънцето и Луната не се местят като неподвижните звезди по паралелни на екватора окръжности, а се отдалечаавт от екватора понякога на север, понякога на юг, връщат се и отново се доближават до екватора? Обяснението на Анаксагор е механистично (Van der Waerden 1968, Иполит, Refutatio I, 8):
„Слънцето и Луната постоянно се връщат, защото те на север се отблъскват назад от студения въздух. Луната се връща по-често, защото тя не може да надделее студения въздух“
Движението на Слънцето и Луната Анаксагор разложил на две компоненти – една паралелна на екватора и една перпендикулярна на него. Това е допустимо разлагане от кинематична гледна точка, но за него той дал съвършено различни обяснения. Следствие от това е, че Слънцето в неговия модел по чиста случайност минавал всяка година по една и съща траектория – връща се към същия тропик, но и към същото съзвездие и заедно с Луната е винаги в пределите на зодиака. Този астрономичен модел е задънена улица, защото той отхвърля математическите закони на движението и предлага случайност за обяснение на движения, които са безкрайно малко вероятно да са случайни. За сравнение с модерните учени, вземете обяснението на Кирхоф (Polya, 1976: 111), който наблюдавал разпределението на спектралните линии на желязото и ги съпоставил с тези на Слънцето. Слънцето излъчвало електромагнитни вълни на определни честоти (това се дължи на факта, че електроните излъчват и поглъщат фотони само с определени, дискретни честоти), но част от тези честоти съвпадали много точно с тези, на които излъчва желязото. – Фиг.2.
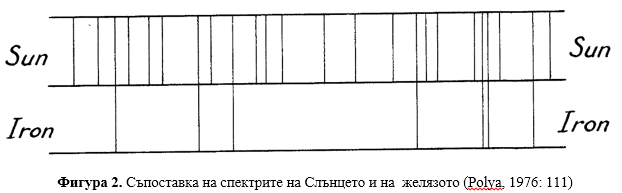
Съществува алтернативната хипотеза, че тези съвпадения на линиите са случайни., т.е. Слънцето не съдържа желязо, което да излъчва тези честоти на вълните. Кирхоф изследвал 60 линии на желязото, и установил, че всяка от тях съвпада с някоя от слънчевите линии. Кирхоф бил сигурен, че няма да пропусне разлика по – голяма от 0.5мм по неговата скала. Средното разстояние между две спектрални линии било 2мм. Ако 60-те линии на желязото са разхвърляни случайно върху картината, каква е вероятността някоя от тях да попадне по-близо от 0.5м до някоя от слънчевите линии? Кирхоф стигнал до отговора на този въпрос, който го убедил, че тук има природен закон, че това не може да е случайно (Polya, 1976: 112):
„… вероятността това съвпадение да е дело на случайност е по-малка от (1/2) на степен 60… Следователно това съвпадение трябва да е резултат от някаква причина и може да се намери причина, която да дава съвършено обяснение на наблюдаваните факти“
Сравнението с обяснението на Анаксагор демонстрира несъстоятелността и ненаучността на неговия подход, който се дължал на нежеланието да приеме наличието на математически закони, произтичащи от Разума, тъй като не вярвал в този Разум (той все пак базира Вихрите като произтичащи от Разума). Желанието да обясни движението на небесните тела без нуждата от единна причинно-следствена връзка се дължи на неговия (частичен) атеизъм, който е априорен, а не следствие на научен подход и доказателства. В онази епоха, с разбирането на универсалния космически ред като произлизащ от първоизточник, за да се обявиш срещу Бога трябва да се обявиш срещу научния метод. Това е и причината Анаксагор да приеме едно безкрайно невероятно обяснение ( с вероятност 0), вместо най-вероятното, за разлика от съвременните учени като Г. Кирхоф. Нещо повече, неговото обяснение дало астрономичен модел, който е съществено неверен и не може да претърпи подобрение. Той е трябвало изобщо да бъде отхвърлен, за да продължи развитието на астрономията, както и всички други механични теории, предлагащи случайността и вихровото движение като обяснение за движението на небесните тела.
Демокрит от Абдера
Той разработил възгледите на Анаксагор в още по-материалистически дух (Van der Waerden 1968: 181). Демокрит отстранил от системата на Анаксагор разума, който според възгледите на последния въвел ред във всичко и придал на веществото вихрово движение. Той оставил всичко на волята на слепия случай, натиска и тласъците и според неговата теория планетите и преди всичко Луната изоставали от звездите, защото те били по-близко до нас и следователно не се увличали силно от вихровото движение на планетите. Той не се и опитал да търси законите на планетните движения, тъй като в хаотичните вихрови движения такива не съществуват. Наличието на „необходимост“ в движението на вихъра при него не е отсъствие на случайност, а множество от необходими причини на мястото на една обща причина, на един пораждащ, математически закон. Привидното противоречие, установено от (Edmunds 1972) между причинност и случайност (chance) не съществува, тъй като има множество от необходими причини вместо една за хаотичните движения. Това множество служи, за да замести общия закон за поведението на небесните тела и е пренесено и в неговия атомизъм.
Неговите възгледи изглеждат съвременни и квантово-механични само на пръв поглед – той отхвърлял математическите закони, а при случайните процеси такива съществуват – вероятностните разпределения не са случайни. Представата за неизменен ред, изникващ от случайните взаимодействия е нещо ново, принадлежащо на съвремието, а не на Античността. Случайните тласъци, предлагани от Демокрит са движени от неговия атеизъм, неговия бунт срещу идеята за Разума като първопричина. Той дори не се и опитал да търси закони за движението на планетите, защото създал своя модел именно срещу тези закони, които тогава са олицетворявали Божественото. Ето как атеизмът и при него не е следствие на научен подход, а причина той да отхвърли научния метод в този случай и да избере безкрайно невероятно обяснение, само за да опише материалистично света. В други аспекти на неговото научно творчество това отхвърляне се оказва плодотворно – неговата космогония се смята за близка до модерните разбирания за теорията на множествената вселена (Danezis et.al., 2010). Това отново се основава на отказа от търсене на първопричина и залагането на слепия случай, поради което съществува безброй много Вселени, всяка от които със свои закони, като реализация на всеки възможен случай. Докато в контекста на астрономичните модели на Слънчевата система това води до отхвърляне на научния метод и приемане на теория с нулева вероятност, то тук това е близко до съвременните физични теории. Много други негови изследвания като това за естетиката, са неповлияни или слабо засегнати от матералистичните му възгледи, с което те не пречат на прилагането на научния метод (както е разбиран в древна Елада).
Питагорейците и Платон
Питагорейската представа за небесата, както писахме по-горе е, че планетите са божествени, одушевени живи същества, които притежавайки разум, извършват своите вечни кръгови движения по математически закони. Това не е примитивно обожествяване и идолизиране, а следствие на логическа необходимост с преподставките, с които тогава са разсъждавали. Навсякъде в Природата се наблюдава ред само там, където има разум, който да го породи, така както хората правят. Геометрията е плод на разума, а движението на планетите по стриктни, кръгови орбити изглежда следствие на разумно действие или първопричина.
По мнението на Ван дер Варден това е по-плодотворният възглед, тъй като подбужда хората със собствения си раузм да търсят тези закони и да определят кръговите орбити на планетите. За разлика от хаоса и случайните движения в представите на Анаксагор и Демокрит, един математически подреден Космос може да се опознае – и точно това е източникът на удивление на Нобеловите лауреати по физика Айнщайн, Уигнър и Шрьодингер. Популярността на материалистическите възгледи е била висока през златния век на просвещението на Древна Елада. Това е време, в което общата образованост сред населението стига своя пик, непостижим за днешния ден – време, в което дори въпроси като този за квадратурата на кръга са били достатъчно разбирани, за да бъдат включени в пиесата „Птици“ на Аристофан. Време, в което всеки е имал свободата и образованието да се усъмни във всичко, въпреки, че съмнението в математичните закони не произлиза от рационален източник, тъй като води до възприемане на най-невероятните обяснения, за да се пренебрегнат най-вероятните. Тежък отговор на това дал Платон в I книга на своя диалог „Закони“(Plato 1999: I):
„Хората казват, че Слънцето, Луната и звездите са планети или скитници; но това е обратното на фактите. Всяка от тях се движи само по една орбита, която е кръгова и не по много; нито най-бързите от тях са най-бавните, както изглежда на човешките очи. Каква обида би било ако предложим на Олимпийските бегачи първият да е на последно място и последният да е на първо! И ако това е нелепа грешка, когато говорим за хора, колко по-нелепо е, когато говорим за Боговете? Те не могат да бъдат удовлетворени от нашето изричане на неверни неща за тях Те не могат. Тогава хората трябва най-малкото да научат достатъчно за тях, за да избегнат безчестието.“
Според Платон, Аристотел и Питагорейците Разумът владее всички неща, като първоизточник и първопричина, поради което и Теофраст бил даден на съд за безбожие, когато поставил Случая на негово място, както изглеждало от неговите думи.
REFERENCES/БИБЛИОГРАФИЯ
Aristotel [350 BCE] N. Gotchev (trans.) (2000) Metaphysics [Аристотел [350 пр.Хр.], Н. Гочев (прев.) (2000). Метафизика, стр.60]
Bogdanov, B. Theophrastus characters – past and present, in Characters, Iztok-Zapad [ Б.Богданов (2016). Характерите на Теофраст – минало и настояще, в „Характери“, Изток-Запад] http://bogdanbogdanov.net/pdf/108.pdf
Germain, Sophie (1914) Mémorie sur les Surfaces Élastiques. In Robert Édouard Moritz, Memorabilia Mathematica (1914), p.211
Danezis et.al. (2010) The Cosmology of Democritus, Bulgarian Astronomical Journal 13, 2010, pp. 140–152, http://www.astro.bas.bg/AIJ/issues/n13/11_EDanezis.pdf
Dunnington, G.W. (2004) Carl Friedrich Gauss: Titan of Science, Literary Licensing, LLC
Edmunds, L. (1972). Necessity, Chance, and Freedom in the Early Atomists. Phoenix, 26(4), 342.
Einstein, Albert (2013). Albert Einstein, The Human Side. Princeton: Princeton University Press, pp. 32-33
Mackay, A. (1991). A Dictionary of Scientific Quotations, CRC Press; 1 edition (January 3, 1991), p.100
Mlodinow, L. (2011) The Drunkard’s walk, BARD [Л.Млодинов (2011). Походката на пияницата, БАРД]
Plato, Panova, N., Gotchev G. (trans) (2006) Laws, SONM [Платон Н. Панова, Г. Гочев (прев.) (2006), Закони, СОНМ.]
Plato, Jowett B (trans) (1999), Laws, Guthenberg project
http://www.gutenberg.org/ebooks/1750?msg=welcome_stranger#link2H_4_0014
Polya, G. (1976) Mathematics and plausible reasoning: Volume I: Induction and analogy in mathematics, Nauka i Izkustvo [Д. Поѝа (1976). Математиката и правдоподобните разсъждения. Том втори – схеми на правдоподобните разсъждения, Наука и Изкуство.]
Taleb, N.N. (2009) Fooled by randomness, Infodar [Н.Н. Талеб (2009). Надхитрени от случайността, Инфодар]
Van der Waerden, B. (1968) Science Awakening, Nauka i Izkustvo, [Ван Дер Варден (1968). Пробуждаща се наука, Наука и изкуство]
Wigner, E., Penkov, B. (ed) (1973). The Unreasonable Effectiveness of Mathematics in the Natural Sciences – in “Problems of modern mathematics”, Vol.1, Nauka i Izkustvo, pp.96-108 [Ю. Уигнър, Б. Пенков (ред.) (1973). Необяснимата ефективност на математиката в природните науки – в „Проблеми на съвременната математика, том I“, Наука и изкуство стр.96-108]






