Рационалност и изчислимост
“Всички най-велики математици отдавна са осъзнали, че представеният в тази книга метод е не само изключително полезен при анализа, но и допринася значително за решаването на физически проблеми. Защото тъй като тъканта на Вселената е най-съвършена и е дело на един много мъдър Създател, нищо не се случва във Вселената, в която някаква връзка между максимума и минимума не се появява.“
Леонард Ойлер”[i]
Историята се повтаря, но като фарс. Ренесансът не възражда, а подменя античните ценности и култура. Рационализмът замества рационалното, като изхвърля от него случайното и шанса. Механичният поглед към света през Просвещението може да се онагледи с подмяната на оригиналното значение на думата αὐτόματος – самостоятелен, необвързан от причини, свободен и следователно случаен. Автоматите са точно обратното – програмирани, детерминистични, изцяло определени от причини и следствия, с повторяеми грешки. Тази подмяна се отразява на всички нива – разбирането на системите като машини, ударението върху индивида като самодостатъчен и свеждането на рационалното поведение до инстинктивното (в икономически и обществен план)
Рационалното поведение според съвременните дефиниции представлява максимизиране на целева функция (например печалбата за тримесечието). То е предопределимо, предсказуемо и програмируемо, защото се свежда директно до физическите закони, докато разумното поведение е свързано с избора и оттам е алгоритмично неразрешимо. Рационалните агенти също както насекомите следват прости, алгоритмични инструкции (яж, моли се и обичай), защото се подчиняват на принцип, аналогичен на този на Мопертюи – „пътят, следван от една физическа система е този с най-малка дължина“. Мопертюи е виждал аналогията в живата природа:
Законите за движение и почивка, изведени от този принцип, са точно същите като тези, наблюдавани в природата, можем да се възхищаваме на приложението му във всички явления. Движението на животните, вегетативният растеж на растенията … са само неговите последици; и зрелището на Вселената става толкова по-великолепно, толкова по-красиво, по-ценното на неговия Автор, когато човек знае, че малък брой закони, най-мъдро установени, са достатъчни за всички движения[ii]
Един рационален агент винаги ще иска да спечели пари с най-малко разходи, да премине по най-късия път, или да работи най-малко за даден резултат. Това е рационално, изчислимо и предсказуемо поведение. Нещо повече, то е детерминистично. Невинаги то дава обаче най-добрите резултати. Проблемът за кучето и вратата е типичен пример[iii]:
Имаме едно куче, една ограда с отворена порта в нея и един кокал от другата страна на оградата. Кучето стои точно срещу кокала, а вратата на значително, но видимо разстояние отстрани. Типичната редукция на задачата за взимане на кокала е:
Стъпка 1. Стигни до оградата
Стъпка 2. Премини през оградата.
Стъпка 3. Вземи кокала
Кучето тук няма успех, защото в общия случай Стъпка 2 е неизпълнима. В математическа форма това е задача за минимизиране на функция (разстоянието до кокала) и това е разделение на серия от стъпки, във всяка от които разстоянието намалява.
Успешната редукция на задачата е следната:
Стъпка 1. Стигни до вратата
Стъпка 2. Премини през вратата.
Стъпка 3. Вземи кокала
Този подход обаче изисква увеличаване в началото на разстоянието, което локално гледано е отдалечаване от целта. Локалното мислене на всяка стъпка не гарантира, че ще изпълним целите си. Ключът тук е да се преобразува физическото пространство в абстрактно, в което разстоянието до кокала намалява с приближаването до вратата.
В математиката този подход е решен по множество различни (по – прости) начини – с добавяне на случаен елемент (кучето се върти около оградата, докато не попадне на и през вратата), с паралелно обхождане (пускане на множество лутащи кучета) и или чрез промяна в представянето на задачата (преминаване в друго пространство)[iv]. Проблемът е с изкуствения и естествен интелект. Хората решават ежедневно по – сложни варианти на тези задачи, като се отдалечават временно от целта си, за да я постигнат, но в по – ежедневните, не абстрактни варианти. В по – малко очевидни ситуации някои хора не успяват да разпознаят, че временното отдалечаване от целта е пътят към нейното постигане. Примери за това са хора, които не желаят да учат, защото това е време, в което не трупат стаж. Това временно отдалечаване от целта не е разпознато като част от траектория към по – високи доходи и/или по – голяма сигурност.
Рационалното поведение може да ни отведе само до оградата, но не и до вратата и оттам до кокала зад нея. Типични примери в икономическия живот са разглежданото като проста дроб от мениджърите съотношение приходи/разходи. Минимизирайки разходите, те се опитват да максимизират съотношението, следвайки принципа на най-малкото действие, частен случай на който е принципът на Мопертюи. Това е поведението, което ще ги отведе до оградата, но не и до кокала. Това не е обмислено поведение, а следване на инстинктите, които всички живи същества имат. Приходите и разходите са свързани, минимизацията на разходите не максимизира приходите. Oт нищо нищо не може да произлезе (Ex nihilo nihil fit) – основен физичен принцип, който рационалното поведение не може да наруши, когато го пренебрегне. Авторът състави примерен тест за мениджъри за този тип мислене:
Тест за мениджъри: Дават ви се
две числа, трябва да кажете кое е по-голямо веднага (без да мислите):
20/3 или 6/1
Друг пример за предсказуемо и рационално поведение е следването само на индивидуалния интерес в колективна среда – във фирмите, в които има годишно оценяване и уволнение на последните по представяне 10%. Всеки такъв служител мисли само за своя интерес, което може да доведе и до фалшифициране на данни, разпадане на екипите и дори да фалира компанията. Това се нарича субоптимизация[v]:
“Оптимизирането на резултата за подсистема по принцип няма да оптимизира резултата за системата като цяло. Тази вътрешна трудност може да се превърне в „трагедията на общината“: изчерпването на споделените ресурси поради конкуренция между подсистемите”
Всеки отделен човек иска да се справи по-добре от останалите, за да оцелее, така никой не се справя добре. Подобно е и изискването всеки отдел от една фирма да е на максимална печалба, но печалбата на фирмата така не е максимална. Отделите за развойна дейност дълго време могат да не генерират никаква печалба, а в кратък период да създада нови технологии, които да донесат милиарди. Тъй като откритията не са предсказуеми[vi], тези отдели изглеждат като мъртъв товар в счетоводните отчети. Всеки алгоритъм би се провалил в опита да изчисли ползата от тях, както и всеки чисто рационален човек и въпреки това тя е видима за разумните хора.
Повечето задачи в реалния живот от този тип не са алгоритмично изчислими. Подобни проблеми се преодоляват в изкуствения интелект, но не с генерирани краен брой прости указания за действие, а по чисто математически път с използването на аналог на човешкия мозък – невронните мрежи. Дори и тогава, създадените програми имат специфични задачи, които не могат сами да сменят без да влязат в безкрайна регресия. Най-простият пример за неизчислимост е следният:
Ако имаме два алгоритъма за генериране на реални числа, едното е 0.9999…, а другото е 1.0000…., въпросът дали са равни, не може да се реши алгоритмично, със сравнение между тях, защото двата алгоритъма, трябва обходят цялата завършена актуална бзкрайност, преди да можем да каже дали са равни или не. Независимо от всичко, човешкия разум в състояние да ги сравни, чрез т.нар. граничен процес – границата на 0.9999 с безкраен брой 9-ки след запетаята е 1-ца и в този смисъл двете числа са равни.
Разумното е в състояние да осмисли това, което рационалното може да повтаря безкраен брой пъти, без да може да даде отговор, очаквайки „накрая“ различен резултат. Рационалното следва плътно определението на Айнщайн за лудост[vii] защото то има фиксиран критерий за спиране, който в много случаи никога не се изпълнява.
Определението, което Айнщайн дава за лудост, напълно съвпада с идеите на Честъртън в Ортодоксия[viii] (Фиг.1):
“Обикновеният човек винаги е бил разумен, защото винаги е бил мистик…. Винаги се е интересувал повече от истината, отколкото от последователността. Ако види, че две истини си противоречат, би приел и двете заедно с противоречието между тях.
Приехме кръга за символ на разума и лудостта. Като символ на мистерията и здравето можем да приемем кръста. Кръгът е съвършена безкрайност, застинала завинаги във формата си. Той не може да се увеличи или смали. А кръстът, макар и да пресича в себе си сблъсъка и противоречието, може да простре четирите си краища до безкрая, без да приеме формата си. Тъй като за център му служи парадоксът, той може да расте без да променя същността си. Кръгът се връща към себе си и се ограничава от себе си. Кръстът се разтваря на вятъра в четирите посоки – той указва пътя на свободните друмници.”

Ще си позволим да видоизменим тезата на Честъртън. Кръгът не е символ на разума и лудостта, а на рационалността и лудостта. Той не е съвършената безкрайност, а съвършената неограниченост, символ на алгоритъм, чиито критерий за спиране не се изпълнява след какъвто и да е краен брой изпълнения. Обикновеният човек не е мистик, а метафизик, някой, който се интересува от смисъла на нещата. Мистицизмът е присъщ на рационализма в неговия краен вариант на формализма (в математиката), при който смисълът се изгонва за сметка на игра със символи по определени правила, в които се превръща разсъждението. Поставянето на символите на пиедестал е истинският мистицизъм.
Парадоксът, за който Честъртън пише е алгоритмично нерешим проблем, който разумният човек решава с прозрение[ix]. Лудостта е изпадане изцяло в рационалното и свеждането на мисленето до алгоритмите.
“Рационалното обсъждане е само по себе си дейност като всяка друга и степента, в която човек трябва да се ангажира с нея, е предмет на рационално решение“
Джон Роулс, Теория на правосъдието[x]
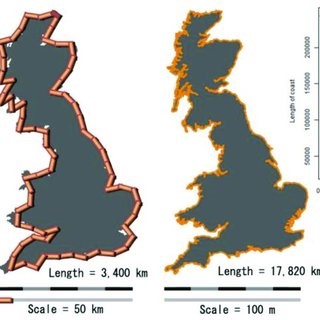
Поставен пред множество почти еднакви избори (като клиент в магазин за обувки) съвършено рационалният агент ще започне да се колебае в избора си, като това може да продължи неограничено. При много близки алтернативи той трябва да има критерий за избор, а за този критерий също трябва такъв и т.н. Така се образува безкраен регрес – нещо, което се смята за прогрес само в математиката и философията. Това е така, когато се опростяват до една функция или едно отношение явления с фрактална природа, които като крайбрежието на Великобритания нямат крайна природа. То няма крайна дължина, както е показал Манделброт[xi]. Ако гледаме крайбрежието в един мащаб имаме една негова дължина, но можем да поискаме да се вгледаме отблизо в него, за да я изчислим по-точно. Вместо да се приближим към отговора (някакво крайно число), ние се отдалечаваме – дължината нараства. С увеличаването на изображението, то не изглежда по-близко до нас, а е подобно на това от по-големия мащаб. Така можем намаляваме мащаба безкрайно и да получаваме все по-голяма дължина.
Рацио от идва от латински ratio – отношение. Гръцките философи-рационалисти от Питагорейската школа, които са били едновременно и мистици, са смятали, че целият свят може да се опише рационално – чрез отношения на цели числа. С намирането на ирационалното съотношение на между диагонала и страната на квадрата, те открили безкрайната рекурсия и фракталността (Фиг.3)
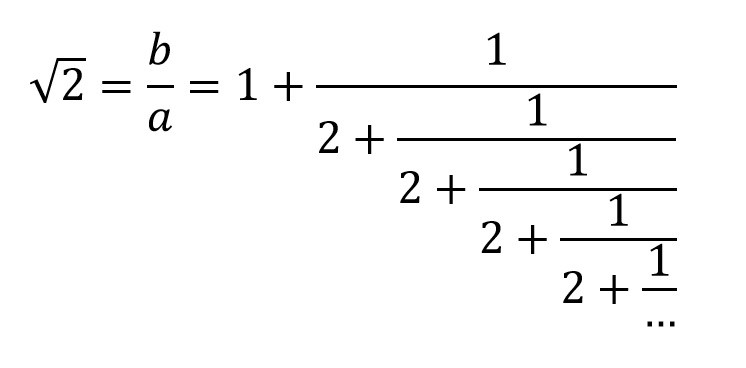
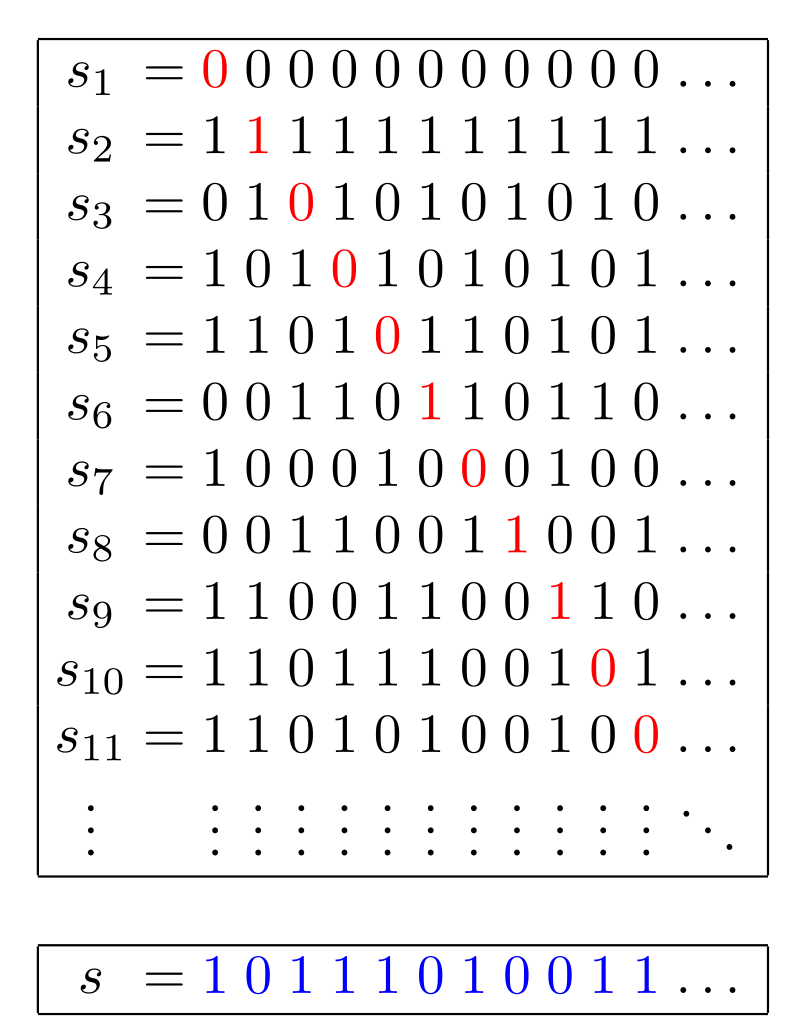
Разумното поведение включва редовното извършване на действия с вероятност с мярка нула. Изборът на рационално число от числовата скала е пример за действие, което не може да бъде имитирано по случаен път, тъй като реалните числа са безкрайно множество, по-голямо от това на рационалните. Ако се опитам да подредим всички реални числа и да им сложим номера, за да ги изброим, ще получим един безкраен списък, който въпреки това не съдържа всички реални числа (Фиг.4). Георг Кантор подрежда реалните числа както е на фигурата с двоично представяне – серии от нули и единици. След това взима първата цифра от първото число и избира различна от нея – в нашия случай първата цифра 0, различната е 1. Така първата цифра на новото реално число е различна от първата цифра на първото. От второто число взимаме втората цифра (Фиг.4) 1-ца и избираме различна цифра – 0. Така новото число се отличава от второто по втората си цифра. Продължаваме така – от третото число взимаме третата цифра и избираме различна от нея, от четвъртото четвъртата цифра и т.н. Процесът може да продължи и безкрайно. Накрая ще имаме число, различно от всички числа в списъка – ще се отличава от първото по първата цифра, от второто по втората и т.н. Въпреки, че списъкът е безкраен, той никога не съдържа всички реални числа. Те са безкрайно повече. Съотношението на броя на рационалните спрямо тези на реалните е 0. Можем да избирам на сляпо реални числа от 0 до 1 без никога да уцелим което и да е рационално като ½, 2/3 или ¾ . Въпреки това ние сме в състояние да посочим произволно рационално число, когато не избираме на сляпо.
Рационалното поведение включва извършването на предимно най-вероятните действия, защото е детерминистично. То е целенасочено, но не себенасочено, защото следва директно физическите закони, които според Шрьодингер в основата си са статистически[xii]. Смисълът, който Шрьодингер влага в това не е свързан с квантовата механика и нейните странности, а с главната роля на термодинамичните закони и това как законите на макроскопично ниво (класическата механика) идват от статистически свойства на поведението на частиците и по-точно от огромния им брой (усредняване на поведението). Това превръща рационалното поведение в известен смисъл в производно на статистическите закони. Поведението на едно животно, което търси храна и на един рационален икономически агент, който иска да максимизира печалбата си, се описват с един и същ математически модел. Няма обаче математически модел, който да описва създаването и разпознаването на математически модели (няма теория на ума).
„Никоя природа освен изключителната не би могла лесно да формулира теория.“
Платон [xiii]
Удивителната способност на човешкото същество да формулира теории с малко или никакви експериментални данни, които после разкриват неподозирано много нови явления, през цялата научна история е загадка може би извън нашите възможности да разберем според Шрьодингер и Уигнър[xiv]. Такива са историите на откритията на Нютон и Галилей, създали теории за механиката на Вселената от два или три, удивително сполучливи опита. Такива са движените от естетически съображения математически открития на Максуел и Дирак, дали много повече от очакваното. Това са действия, които изглежда излизат извън алгоритмично изчислимото и логически програмируемото. Рационалното поведение се подчинява на математическата теория, разумното поведение използва и развива математическа теория.
Рационалното е логично, разумното е творческо:
„Не, не, вие не мислите, вие просто сте логични“
Нилс Бор[xv]
Рационалното поведение може да е логично, без да извиква логически стъпки в разсъжденията, да е логично видяно отвън, като следване на закономерност, на максимален принцип. Разумното не може да е логично отвън без да е логично отвътре, но може да е логично отвътре, без да е логично отвън – заради свободата на избора – възможността да спреш, когато поискаш обикалянето в кръг около истината.
Рационалното произвежда противоречия, които разумното избягва, тъй като първото е статично, а второто – динамично. Пример за това е тезата за силен изкуствен интелект – всичко, което ние правим, може да се повтори от алгоритъм. Няма значение дали носителят е мозък, или компютър или механично устройство с колела и тръби, дали е цифров или аналогов, дали е органичен или не. От значение има само логическата структура на алгоритъма. Това въвежда дуализъмix както при философията на Декарт – съществува отделно вещество на разума, което не се смесва с материята. Разумът е нематериален, той е алгоритъм, абстрактна, Платонова идея, напълно отделена от физическата идея. Така опитът да се избяга от мистичното и да се сведе човешкия разум до нещо „тривиално“, да се покаже, че и машините могат да имат разум, да възтържествува рационализмът, всъщност води към идеите на Платон и до нематериално обяснение на разума, до мистицизъм.
Разум и време
„Всеки разумен избор би трябвало да се прави при съответно отчитане на миналия опит и бъдещите последици.“
Дьорд Поѝа,
Схеми на правдоподобни заключения[xvi]
Рационалното поведение е фокусирано, а разумното е дифузно. Рационалното е в настоящето и малка област от пространството, разумното се осланя на опита, мисли за дългосрочните последици и за далечните последствия. „По делата ще ги познаете“ е рационално, „По плодовете ще ги познаете“ е разумно. Мъдростта, това е опитът, натрупан чрез мислите и действията на разума през времето. Рационалното поведение е действие според ситуацията, защото е подчинено на фиксирана крайна цел и оттам на фиксирана структура, разумното поведение е действие според принципи, които не се изменят, но структурите (алгоритмите) се променят и еволюират.
„Човек е направил поне едно начало на откриването на смисъла на човешкия живот, когато засади дървета, под чиято сянка той добре знае, че никога няма да седне“
Елтън Трублъд[xvii]
Рационалното в крайна сметка е аморално, моралността е независимо измерение, независим компонент, който трябва да се включи, за да го сдържа. Утилитаризмът в крайната му форма и идеите за канибализъм срещу глобалното затопляне са примери.
Разумното поведение е задвижено от морала, то си поставя цели, обусловени от него, като оцеляването на вида. То вижда напред в бъдещето и вижда надалеч в пространството. Целта не е една и не е само за един човек. Няма изчислима целева функция, която да се максимизира.
Рационалното избягва времето, вижда го като част от геометрията на света, за него има само вечното сега. Разумното се движи във времето – от миналото към бъдещето, само така може да обхване повече от една гледна точка, да бъде нелокално, да вижда връзките между отдалечените във времето и пространството явления, да бъде чувствително и за това, което би могло да стане, не само за загубите, но и за пропуснатите ползи.
Рационализъм и консерватизъм – кое е така и кое не е
Писахме и преди за връзката между консерватизма и опита[xviii]. Ако законът за най-малкото действие е консерватизмът на физическите системи, то в политиката той е свързан с това допълнително усилие, което ни отклонява от минимума, тъй като целта не е запазване, а продължаване – на вида, на морала, на традициите, на смисъла. Рационализмът е пряко следствие на опошляването на античната гръцка култура с нейната строга, интуитивна логическа основа и неприемането на актуално безкрайното[xix] , със замяната на идеята за „цялост“ с механистично разбиране за света като гигантски часовник. Той е несъвместим с разумността на консерватизма, който приема Времето, изгонено от рационалистичната визия за часовниковата Вселена. Каква ирония, нали? Именно чувството за ирония е онова неизчислимо нещо, липсващо на рационалността, която в безкрайността се превръща в лудост, но е присъща на разума, който рефлектира върху себе си и миналите си състояния, не в статичен цикъл, а в спираловидното движение напред във времето с багажа на миналото на гърба. Това е част от тема, която в малка или голяма степен е разисквана и анализирана от много специалисти и преди. Нещото, за което не е писано е какви въпроси се задават при рационалистичното и разумното, консервативното. Те се проявяват различно и според въпросите, които задават при търсенето на информация:
Да се отговори на въпроса „Кое не е така?“ е безкрайно по-трудно, отколкото да се отговори на „Кое е така?“
Теоремата на Гьодел и проблемът за спирането на Тюринг показват, че в много случаи можем да генерираме алгоритмично отговори на „Кое е така?“ Можем да разберем с краен брой стъпки кой елемент принадлежи на множеството, спира ли n-тата машина на Тюринг T(n), но никакви алгоритми не могат да генерират отговори на въпрос за елементи, които не принадлежат на множеството, нито може да даде съобщение от вида „T(n) не спира“.
Както е открил (в известен смисъл) и Бояй (заедно с Гаус и
Лобачевски), можем да проверим с краен
брой стъпки, че две прави се пресичат, и къде, тъй като могат да се пресекат
само в една точка, но не можем да докажем, че не се пресичат, тъй като трябва
да проверим всичките им точки, който са безброй. Въпреки това човешкият ум е
способен да „прозре“ истината, както пише Роджър Пенроуз – да види,
че правите са успоредни и, че няма обща точка. В този смисъл задаването на
въпроса „Кое не е така“ е ръкавица, хвърлена към логиците и
формалистите от разумните хора, които разбират, че има нещо
„Божествено“ в знанието. Да се пита „Кое е така?“ е
либерално, рационалистично и формалистично, да се пита „Кое не е така“
е консервативно, традиционалистко и мета-епистемологично.
[i] https://www.dropbox.com/s/o09w82abgtftpfr/1933-oldfather.pdf
[ii] Chris Davis, Idle Theory, https://web.archive.org/web/20060615043538/http://www.idlex.freeserve.co.uk/idle/evolution/ref/leastact.html
[iii] https://www.researchgate.net/publication/320685777_Freedom_Brexit_and_AI_In_Bulgarian
[iv] P. Venkataraman, Applied Optimization with MATLAB Programming, 2nd Edition, Wiley and Sons, 2009, ISBN: 978-0-470-08488-5
[v] http://pespmc1.vub.ac.be/SUBOPTIM.html
[vi] Sinatra et.al. Quantifying the evolution of the individual scientific impact, Nature, Science 04 Nov 2016: Vol. 354, Issue 6312 https://science.sciencemag.org/content/354/6312/aaf5239
[vii] Лудост: да правиш едно и също нещо отново и отново, и да очакваш различни резултати.
[viii] Гилбърт Кийт Честъртън, Филипина Филипова (прев.) Ортодоксия, Омофор, 2018
[ix] Р. Пенроуз, Новият разум на царя, гл. Истина, Доказателство и Прозрение, СУ „Климент Охридски“, 1998
[x] H. Smith. Deciding how to decide: Is There a Regress Problem? https://philosophy.rutgers.edu/joomlatools-files/docman-files/Deciding_How_To_Decide.pdf
[xi] B.Mandelbrot, How Long is the Coast of Britain, Statistical self-similarity and fractional dimension, Science: 156, 1967, 636-638 https://users.math.yale.edu/users/mandelbrot/web_pdfs/howLongIsTheCoastOfBritain.pdf
[xii] E. Shrödinger, The Statistical Law in Nature, Nature, volume 153, pages704–705 (1944) http://www.whatislife.ie/downloads/What-is-Life.pdf
[xiii] https://www.facebook.com/ltomov/posts/10157337482479204
[xiv] Ю. Уигнър, Необяснимата ефективност на математиката в природните науки, https://drive.google.com/file/d/1EjSrrLH0qmsJCASZD46ngvJAv313BB1L/view?usp=sharing
[xv] https://en.wikiquote.org/wiki/Niels_Bohr
[xvi] https://drive.google.com/file/d/1oAdhxDh-p1YH0bSeytc1cNftZD7amjEc/view?usp=sharing
[xvii] Elton Trueblood (1951), The Life We Prize, Harper, p.58, https://books.google.bg/books?id=OGEFAAAAMAAJ&q=shade+trees&redir_esc=y Retrieved at 1-2-2019
[xviii] https://conservative.bg/conservatizma-liberalizma-slojnite-sistemi/
[xix] https://www.researchgate.net/publication/335335512_Problemt_za_markata






