Научните изследвания като рисков актив. Безкрайната ефективност на научните изследвания
Годината 1905 е знаменателна в историята на физиката. Наречена е annus mirabilis Витанов (2018), Айнщайн и др. (2018) – годината на чудесата. Една след друга излизат няколко статии по теоретична физика на Алберт Айнщайн – една, в която с помощта на статистически методи доказва съществуването на атомите и която отваря направлението статистическа физика; статия, обясняваща фотоелектричния ефект, при който светлината предизвиква отделяне на електрони и електричен ток само над определена честота на вълната. Това е свързано с дискретната ѝ природа на състояща се от фотони – подкрепа за изследванията на Планк, подпомогнала създаването на квантовата механика. Накрая идва и статията, с която той създава специалната теория на относителността, която постулира абсолютността на скоростта на светлината и принципа на относителността, според който законите на физиката остават едни и същи за всяка равномерно движеща се инерциална отправна система (прословутата симетрия, наричана с по – грозния термин „инвариантност“). Последствията от тези постулати са свързани с относителността на времето спрямо скоростта на движение на наблюдателя, със зависимостта на масата и размерите на движещото се тяло от скоростта му и с прословутото уравнение, свързващо масата и енергия през квадрата на скоростта на светлината (още една статия от 1905 г.) (1). Уравнение, само по себе си възможно благодарение на теоремата на Питагор, в чест на която казват, че принесъл в жертва над сто вола, когато я доказал.
![]() (1) [i]
(1) [i]
Трудно е да се даде крайна стойност на ползата от тези три статии на Айщайн, които далеч не изчерпват при това неговия принос, най – големият триумф на когото е общата теория на относителността. Глобалната позиционираща система GPS не би била възможна без сателити, които при тяхната скорост на движение се нуждаят от релативистични корекции на пресмятанията, за да запазят орбитата си. Общата теория на относителността предсказва забавяне на времето близо до тяло с голяма маса и съответно разлика между часовниците на земята и тези, във висока орбита. Финансовите и други ползи от GPS с времето растат неограничено, съответно дори само тази отделна полза от научните изследвания на Айнщайн е безкрайна.
Всички свои изследвания до 1905 г. Айнщайн прави, докато работи като чиновник в патентно бюро в Швейцария. Срещу минимална държавна инвестиция от страна на Германската империя и Швейцария, изразяваща се в помощ за неговото образование, човечеството получава безкрайна възвръщаемост на своите вложения. Своите открития Айнщайн прави в свободното си време, тласкан от интелектуалното любопитство, присъщо на homo sapiens sapiens, от вътрешния подтик да се търси и намира ред в околния свят, който прави математиката естествена за всеки човек, а не чужда, както много хора смятат. Както Харди 1971 посочва, шахът е чиста математика, както и бриджът „на едно по – ниско ниво“ или кръстословиците. Естественото любопитство към скритите закономерности зад проявленията във външния свят е това, което е тласкало Айнщайн, Гаус, Архимед и Нютон, не обещанието за финансова награда. Според Харди математиците са амбициозни хора, но амбицията при тях не е финансова, а свързана със създаването на трайни резултати, които ще ги надживеят, нещо особено вярно за чистата математика, но и за физиката, химията, биологията и другите природни науки. Луи Пастьор или Чарлз Дарвин са записали имената си с не по-малки букви в книгата на вечността, независимо от това как техните открития и теории биват видоизменяни и потенциално отхвърлени във времето. Пастьоризацията и ваксините са спасили десетки милиони животи и имат същата безкрайна полза, ако се разглежда в безкраен хоризонт от време напред, както и теоремата на Питагор. Една ваксина може да замени друга след време, но идеята за ваксинация е вечна и се доближава до математическото творчество. Математиците, казва Харди, работят с идеи:
„Математикът подобно на художника или поета е създател на образци. Ако неговите образци са по – трайни от техните, то е защото са направени от идеи… Бедността на идеите, изглежда, едва ли влияе върху красотата на стихотворния образец. От друга страна един математик не разполага с друг материал за работа освен идеи и поради това образците му имат изгледи да траят по-дълго, защото идеите по-малко се износват с времето, отколкото думите“.
Теоремата на Питагор (2), Фиг.1 като идея е открита още във Вавилон, но доказана в Гърция. Значението ѝ е всеобхватно – без нея не може да се измерва разстояние в пространства, които далеч не се ограничават с физическото – съществуват и функционални, безкрайномерни[ii] пространства. Съществуват много други „норми“ освен дефинираната чрез нея, които я обобщават и следователно се нуждаят от нея. Те се прилагат във всички области на математиката, които видимо се допират до приложенията – от хармоничния анализ (комуникации), теория на вероятностите и статистика (икономика, военна наука), функционалния анализ (икономика, електроника и оптика през квантова механика, теория на управлението, балистика, следящи системи, круизен контрол на автомобили) през каквото друго се сети човек, създадено от хората и използващо електромагнитна енергия за захранване. Ползите от теоремата на Питагор са много повече, отколкото дори от теорията на Айнщайн, а това е чиста математика – умозрителни, абстрактни разсъждения върху обекти, нямащи точен аналог в реалния свят – точки, които нямат размери, прави, които имат само дължина, която е безкрайна, окръжности, чиято дължина е трансцедентална[iii] и не може да се изрази с краен брой елементарни операции включващи извличане на корени.
![]() (2)
(2)

Фигура 1. Теоремата на Питагор в „Елементи“ на Евклид на гръцки от IX век[iv]
Безкрайният хоризонт на научните изследвания
Няма по – внушително предупреждение за онези, които биха желали науката и изследванията да са ограничат с това, което е очевидно полезно, от мисълта, че коничните сечения бяха изучавани в продължение на 18 столетия само като абстрактна наука без никакви изгледи да бъдат оползотворени, освен да задоволяват жаждата на математиците за знания, и че чак накрая на този дълъг период на абстрактно изучаване се разбра, че те са разковничето на най – важните закони на природата.
А. Уайтхед[v]
Основната, единствената цел на научните изследвания е истината. Не истината за това какво в действителност се случва в природата, нито защо, а знанието за природните явления, което научните изследвания дават. Знание, което позволява да предскажем петурбациите в орбитата на Меркурий или завръщането на Халеевата комета във физиката; каква ще е реколтата от зърно в дадена година в земеделието; кое лекарство ще помогне за дадена болест в медицината и т.н. Както Анри Поанкаре, така и Феликс Клайн 1973 наблягат на идеята, че науката има крайна цел истина, която носи полза и която е единствено достъпна посредством научния метод:
„С това недоразумение в широките кръгове е свързано и едно друго, погрешно в основите си схващане за математическото естествознание, което твърде често се застъпва от чистите теоретици. Касае се за мнението, че тази наука и особено аналитичната механика имат за цел да „обяснят“ природата. (Тук бих искал да посоча статията Das Prinzip der kleinstein Wirkung (Принципът на най – малкото действие) от Планк в тома по физика на „Kultur der Gegewart“). На това мнение трябва да се противопостави схващането, че въпреки значението, което може да са имали телеологичните тенденции за развитието на науката, съвсем не е задача на естествознанието да открива свръхестествени „цели“ в природата и даже да привлича такива цели за обяснение на явленията, но, че разбира се, науката може да се свърже с една цел, поставена от самия човек, за чието постигане му е в помощ. Не обясняване на природата, което в последна сметка е невъзможно, а овладяване на природата е нейната истинска задача. Никога не бива да се забравя, че съществува една съзидателна техника, която превръща в дело положенията на теоретичната наука.“
Истината, която е достъпна през научния метод, въпреки всичко подлежи на безкрайно доближаване чрез все по – сложни теории и все по – прецизни експерименти (в емпиричните науки), поради което хоризонтът на научните изследвания е безкраен. Безкраен е и максималният период, след който дадено откритие може да стане полезно. В случая с коничните сечения, както пише големият математик и философ А. Уайтхед, това е период от около 2000 години.
Търсенето на истината има известен метафизичен аспект, поради което научните изследвания в Западна Европа векове наред са били под шапката на Католическата църква, която създава първите университети в Болоня, Оксфорд, Кеймбридж, Париж и др, еволюирали от католически и манастирски училища като това, в което Тома от Аквино пише своите трудове. Схоластичната традиция, която последният завещава, се опира на Аристотел и неговата концепция за наука – търсене на истината по умозрителен път посредство закона на необходимото или вероятното, по пътя на логиката, за първи път формализирана в неговите Аналитики. Нейното наследство намира своя път в единствената наука, която е априори независима от опита – математиката. Това е теория на множествата, за която пише великият математик и създател на математици Феликс Клайн (1973):
„Идеалът за строгост исторически не е имал винаги едно и също значение за развитието на нашата наука; по-скоро в зависимост от условията на епохата той е съвсем различен. През време на голяма продуктивност поради бързото темпо и ръста на развитие той изостава на по-заден план, за да бъде отново застъпен в един по-следващ критичен период, който налага анализиране на добитите съкровища. Да си припомним времето на създаване на диференциалното и интегрално смятане през XVIII век, когато наред с незадоволителната обосновка се появяват на бял свят и някои направо погрешни твърдения, резултат на живата и напираща фантазия и на стремеж към откривателство; или да се обърнем към възникването на теория на алгебричните криви през XIX век. В противовес на това да си припомним времето на схоластиката, когато незначителната продуктивност беше свързана с най-силно изразена строгост на критичното и диалектично мислене. Твърде несправедливо схоластиката е често най-презрително осъждана като безплодно, потъващо в празни спекулации направление на духа. Тъкмо нашето съвремие не би могло да се съгласи с тая повърхностна присъда, която може да има за източник чуждата ни мистична и метафизична основа, присъща на всички творения на тази епоха. Съблечем ли тези одеяния на схоластичните спекулации, които на пръв и повърхностен поглед изглеждат чисто теологични празнодумства, тези спекулации се оказват често най-конкретни представи за това, което днес означаваме като „теория на множествата“. Наистина, самият Георг Кантор, създателят на теория на множествата е отнасян към школата на схоластиците. Обръщайки поглед назад, трябва да кажем, че малко време духът на критиката, стремежът към най-тънко разлагане на всеки мисловен ход – „идеалът за стргост“ – е бил тъй жив, както по време на схоластиката.“
Парадоксално, стремежът към максимална логическа строгост на два пъти спира развитието на математиката. Първият път е когато в древна Елада откриват ирационалните числа, които са пречка за създаването на логически непротиворечива основа на математиката. Това ги кара да сменят аритметичния подход с геометричен, сумиран в книгите Елементи на Евклид (2007) – и особено в теория на пропорциите, чийто автор е Евдокс, най-великият гръцки математик след Архимед.
Тези университети, също както академията на Платон и други в древна Елада, са били напълно откъснати от всякакви дневни, месечни, годишни или петгодишни планове за приложения и ползи и въпреки това, ползите от тяхната работа са неизчислими. Смъртта на Архимед от меча на римски легионер е символична за разликата в нагласите на двете цивилизации. Римляните са практични, инженери и строители, но не и мечтатели и теоретици и поради това – рядко изобретатели. Създадените от него устройства като архимедовия винт, легендарното параболично огледало, фокусиращо слънчевите лъчи в точка, с което се твърди, че изгарял корабите, както и усъвършенстването на катапултите довели до победи за Сиракуза над римляните, преди окончателното ѝ падане. Рим създава нови и подобрява много гръцки технологични постижения, но те оставят забравени в ранното Средновековие, поради липса на афинитет към отвлечените разсъждения на математиците и оттам – липса на систематична научна теория зад тях. Безкрайният хоризонт е само пред научните открития, пред технологичните новости той е краен, пример за това е историята на изчислителните машини и бурното им развитие – днешните смартфони са по – мощни от суперкомпютрите преди десетилетия.

Фигура 2. „Дайте ми опорна точка и аз ще преместя света“ . Тази фраза на Архимед демонстрира способността на мисълта да обхване безкрайното. Тя стои зад всички големи постижения в математиката като проява на въображение над всякакви граници
Ролята на случайността в научните изследвания
„Случаят владее всички неща“
Теофраст
„Най – великият изобретател на всички времена е случайността“
Марк Твен
Какво представлява фабричното производство? Според теорията и опита на У.Е.Деминг (2014) като консултант в стотици предприятия, производството в индустрията е предсказуем процес, когато е стабилен – еднотипни, повтарящи се и съответно автоматизирани действия, водещи до очаквани резултати в рамките на една контролируема вариация, при правилно отношение към доставчиците. Прилагането на статистическото управление на процеси превръща производствения процес в нещо, което може да се планира и залага в отчети и стратегии – едногодишни, двугодишни, петгодишни.
Научните и технологични изследвания не приличат по нищо на това. Никой не е предсказал самодвижещи се коли. „Ако питах клиентите какво искат, щяха да кажат – искаме по-бързи файтони“, казал Хенри Форд. Никой не е очаквал откритията на Исак Нютон в математиката, физиката и оптиката, без които никое съвременно инженерно дело не би било възможно ( математическият анализ, рефлекторният телескоп, законът за всемирното привличане, принципите на механиката). Никой не е „предсказал“ годината на чудесата 1905, нито квантовата механика, теорията на относителността или появата на ваксините. Когато Макс Планк заявил на близо седемдесетгодишния професор Филип Жоли, че иска да се занимава с теоретична физика, той го посъветвал да се откаже, тъй като в общи линии тя била завършена – по Конобеев и др. (1983).
Откритията на Нютон са повлияни от случайността, както знаменитата история с ябълката намеква. Нищо от това, както и машините на Архимед не е могло да се планира, защото, ако можеше, те щяха вече да бъдат открити. Това са неизвестните непознаваеми. Както Марк Твен пише, няма по – голям изобретател от случайността – нещо, известно още на Аристотел и на неговия наследник като ръководител на перипатетическата школа Теофраст – в Богданов (1968). Значението на шанса за скокообразния напредък в знанието и технологиите е разгледано в McCay-Peet and Wells (2017), като един от типичните примери е откриването на структурата на ДНК от Уотсън и Крик, откриването на лазера и много др. Случайността и шансът, обаче не участвуват само в големите открития, но и в стъпките към тях, както и Талеб (2009) отбелязва – това е рационалният процес проба-грешка[vi]. В книгата „Физиците продължават да се шегуват“ е разказан анекдот, илюстриращ природата на научните открития, при които т.нар. Serendipity[vii] играе главна роля:
Много хора посочват, че процесът на превръщането на хипотезата в научно откритие се илюстрира много добре с примера за откриването на Америка от Колумб. Колумб е бил обзет от идеята, че Земята е кръгла и може да достигне Източна Индия, като се плува на запад.
Обърнете внимание на следното:
а) идеята по никакъв начин не е била оригинална, но той получил нова информация;
б) той е срещнал огромни трудности както в търсенето на лица, които да го субсидират, така и непосредствено в процеса на провеждането на експеримента;
в) той не е намерил нов път за Индия, но затова пък намерил нова част от света;
г) независимо от всички противоречащи на това доказателства, той все пак вярвал, че е открил път за Изтока;
д) през живота си не е дочакал нито особени почести, нито съществено възнаграждение;
е) оттогава насам са намерени неопровержими доказателства, че Колумб не е бил първият европеец, достигнал Америка.
Научните и технологични открития следват модела, описан от Талеб в Черния Лебед – това са внезапни и непредсказани събития, понякога с огромни последствия, като Нютоновата механика и първата ваксина, но най-често с по-скромен размер, като безопасната игла и куфарите на колела. Второто е пример, който и Талеб посочва – колелото е известно още от Шумер, но идеята за куфар на колела е относително нова. Колелото е познато в Америка преди Колумб, но не и неговото приложение за транспорт, било е само играчка. Събития, които изглеждат очевидни, след като са се случили, не са били такива. Понякога процесът на развитие, водещ до дадено откритие отнема хилядолетия, въпреки, че преходът от появата до реализацията на приложеният изглежда елементарен, след като те са намерени. Откритията се случват на скокове, чиято поява както в пространството, така и във времето е най-често изненадваща. Вероятността даден изследовател да направи своето голямо откритие е една и съща през целия му активен живот Sinatra (2016), което прави невъзможно надежното ранно разпознаване на бъдещия голям учен. Подобни дългосрочни прогнози, дори базирани на IQ и други измерими показатели, ще са в най-добрия случай равни на хвърлянето на монета. Това прави управлението на рисковете в научните изследвания особено трудно, като съвременният модел, който се следва е точно обратният на верния.

Фигура 3. Пристигането на Колумб в Америка, която смятал за Източна Индия, картина на Иван Айвазовски, 1893
Управление на рискови инвестиции в науката
Управлението на високорискови инвестиции (като тези в ИТ сферата) в практиката често взема формата на евристичното правило 1/n. Целта е парите да се разпределят върху колкото се може повече различни начинания, което и налага равномерността. Причината е, че всяко поотделно има много малка вероятност да се случи (зад всеки успял стартъп има хиляди неуспели), но когато се случи, печалбата няма практическа горна граница – примерите са много, от Гугъл, през Фейсбук до пика на стойността на Биткойн. Целта е тук да не се пропусне изкачването, както пише и Талеб. По – добре е да вложиш по малко пари навсякъде, отколкото по – големи суми „почти навсякъде“ Научните и технологични изследвания са с непознаваеми резултати, непредсказуеми, зависят много и от късмета. Това е творческа дейност, при която се създават нови идеи и техни реализации, като тяхната същност очевидно е неизвестна предварително, а последствията са неоценими. Както дадохме пример по – горе, взет от Талеб, приложението на колелото в транспорта изобщо не е било осъзнато при американските индианци, а от колесниците до куфарите с колела са изминали 3 хиляди години. Коничните сечения са добавили своята стойност 18 века след началото на техните изследвания. Безкрайната полза от дадено откритие може да дойде и след произволно голям период от време, при това от неочаквано място, защото знанието е мрежа, изкуствено разделена на отделни науки и изкуства. Така например безобидните според Готфрид Харди занимания по теория на числата се оказват ключови за криптографията, като допринасят и за развитието на компютрите чрез работата на Алан Тюринг и разработените от него машини Booker (2016). Пак Харди по случайност става създател на направлението популационна генетика поради следобедните си игри на крикет Edwards (2008). С малко помощ от страна на ученическа математика (както той се изразява), Харди показва, че доминантните алели имат относително стабилни пропорции с рецесивните през поколенията, в отсъствията на външни смущения – един неинтуитивен резултат с дългосрочни последствия за развитието на науката, без нужда да се използва висша математика. Откритието е станало възможно поради сплотеното общество на Кеймбридж и честото общуване между специалистите от различни области. В съвременните университети комуникацията е по – слаба и това възпрепятства научните открития, особено тези, които зависят от приложението на математиката в природните и обществените науки.
Непредсказуемата природа на научните открития, която се проявява в това, че не може да се предскаже кой индивид или колектив ще направи дадено откритие, на каква възраст ще бъдат, какви са техните лични характеристики и качества, какви ще са дългосрочните последствия от откритието, какви приложения ще намери и кога ще се намерят те. Всичко това превръща инвестицията в наука и технологии в рисково инвестиране, което би следвало да се управлява коректно, чрез хеджиране – инвестиране в много на брой хора, с очакването по – голяма част от тях да не допринесат съществено, но малцината, които допринесат, да получат огромни ползи, без горна граница, които да компенсират многократно загубените пари от другите. Това е, като да имаш безкрайно математическо очакване, като в 999 случая губиш крайна сума, а в хилядния случай правиш откритие с безкрайни ползи за безкраен период от време. Инвестирането се прави не в проекти, а в Хора, не формално, а възоснова на качествата на изследователите, доколкото може да се съди за тях по външни белези – например каква е мотивацията им – страстта им, квалификацията и т.н. Учените с потенциал за големи открития притежават истинското любопитство към устройството на света, което Файнман култивира толкова старателно и което Хилберт изразява с фразата:
„Ние трябва да знаем – ние ще знаем!“
Тази фраза е отговор на ignoramus et ignorabimus (ние не знаем и няма да знаем), идеята за ограниченото научно познание – един позитивизъм, който колкото и да е нереален, е все пак движещата сила на изследователите и на научния и технологичен прогрес. Границите на познанието непрекъснато се изпитват, разкъсват и разширяват в един безкраен (както Паскал пише) процес.
Измерване на неизмеримите научни резултати
В правилната политика отсъствуват краткосрочни атестации и наукоподобната наукометрия, защото вероятностните характеристики на откритията обезсмислят подобни опити за ранно хващане на успешните учени. Нещо повече, от теория на игрите е известно, че атестиране на брой публикации предизвиква създаване на брой публикации – това, което се измерва, се увеличава, вместо това, което сме искали да увеличим. Получава се инфлация на количеството и дефлация на качеството. Това е известно като закон на Гудхарт (1986):
„всяка наблюдавана статистическа регулярност изчезва, когато се поставя под натиск с цел управление“
Системата постига целите, които са ѝ зададени – Biagoli (2016), не тези, които се имат предвид. Дължи се на това, че измерването на нещо е негова проекция, а не самото нещо и двете не са взаимозаменяеми. Увеличаването на научните резултати повишава наукометричните показатели, но повишаването на наукометричните показатели не означава, че има увеличени научни резултати. Възнаграждаването на брой статии или проекти прави голям брой статии с намалено качество и проекти с по – малък обхват. Съществуват стотици учени, които публикуват средно по една статия на пет дни!
Нещо повече, годишното и дори тримесечно отчитане заменя безкрайния хоризонт с краен и научната продукция с полуфрабрикати. Взимането на решения само по последни данни може да превърне управлението в случайна разходка Томов (2017).
Много често се случва резултатите на даден учен да станат ясни след смъртта му, както в случая с Галоа и абстрактната алгебра. Галоа умира на 20 години в дуел за жена. Преди това на няколко пъти претърпява неуспех в опита си да даде своите две статии, описващи неговата теория – Коши му предлага да ги обедини в една и да влезе в състезание за голямата награда по математика на Френската академия на науките; след това той не успява да влезе в Ecole Politechnique, поради това, че неговият изпитващ не е бил на неговото ниво на компетентност, което разгневило Галоа. След това той успява да влезе в Ecole Normale и дава своя ръкопис на Жозеф Фурие, който за съжаление почива скоро след това и ръкописът се загубва. Бурният живот на Галоа го отвежда за шест месеца в затвора и е изгонен от Ecole Normale; по – късно Поасон го моли да даде своята теория на уравненията, което Галоа прави. Поасон заявява, че тази теория е „неразбираема“. Галоа умира в дуел скоро след това, прострелян в корема и изоставен от опонента си и собствените си секунданти, намерен от минаващ наблизо фермер. Вечерта преди дуела той написва прочутото си писмо Galois (1846), в което описва своите идеи. Херман Вайл (1969) казва за писмото:
„Това писмо, ако се съди по новостта и дълбочината на идеите, които съдържа, е може би най-същественото писание в цялата литература на човечеството.“
Ръкописът на Галоа е публикуван през 1846 г, 14 години след неговата смърт, благодарение на Лювил, а практическите приложения стават видими един век по – късно, напълно неочаквано в квантовата механика (преди това в кристалографията) – феномен, който кара Нобеловия лауреат Юджин Уигнър да напише статия за удивителната ефективност на математиката в природните науки[viii].
Историята на откритията на Галоа и посмъртния кредит, който получава, изпълнена и движена от случайността, далеч не е отклонение от нормата. В наши дни китайският математик Жанг, който направи пробив в т.нар. хипотеза за простите числа близнаци[ix] ( която казва, че съществуват безкраен брой съседни прости числа ) успява на 59 години да намери място в академията – преди това е игнориран и подминаван и дори е работил дълго време като шофьор на такси. Това е пример за „изкачване“, което е било пропуснато, защото инвестициите не са били разпределени върху достатъчно много хора, но също и, че не може да се съди за хората по повърхностни белези, когато трябва да се правят сложни прогнози за нещо толкова далечно от предсказуемия свят на манифактурата. Галоа не е успял да влезе във френската академия на науките, а Жанг да стане професор. Гений от най-високо ниво като Рамануджан изпраща своите ръкописи на петима видни математици и само Харди му обръща подобаващо внимание, като го взима при себе си в Кеймбридж за дългодишно плодотворно сътрудничество с него и Литълууд. Стивън Уайнбърг, който предлага модел, обединяващ слабото и електромагнитно взаимодействие, няма никакви цитирания през първите 6 години след публикуването на статията си, с която печели Нобеловата награда – Фиг.4.
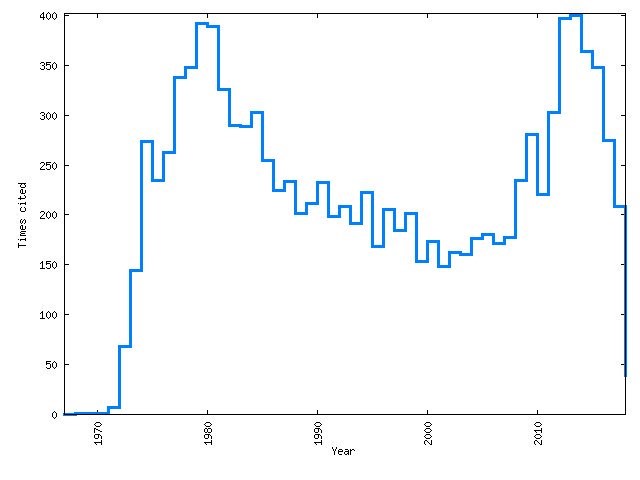
Фигура 4. Цитиране по години на статията на Стивън Уайнбърг „A Model of Leptons“, втората най-цитирана статия в INSPIRE[x]
Едва след експерименталното потвърждение на неговата теория започват и цитиранията, а по – късно идва и Нобеловата награда. През тези няколко години, той би бил неизбираем за хабилитирана позиция по съвременните критерии. Наукометрията е опит за измерване на липсата на оригиналност на една идея – статията на Айнщайн за специалната теория на относителността също почти не е била цитирана дълго време след 1905 г. Pratt (2006). Примерите от този тип подсказват, че е възможно липсата на цитирания да носи информация за оригиналност, а ранните и бързи цитирания е възможно да подвеждат. В крайна сметка цитирането не е друго, освен проявен интерес от други учени към разработваната от даден учен или колектив тема – едно взаимно съизмерване в мрежа, а не по абсолютен, метафизически критерий. Не Истината, а истината през очите на другите хора с непълна информация и ограничена рационалност, както и личното им отношение към автора мерим.
Мястото на научните институти в научните изследвания
Някои научни идеи, възникнали още по времето на Лайбниц, т,е. преди около 250 години, едва сега намериха приложение в промишлеността. Може ли някоя фирма или правителствено учреждение с техните грижи за незабавното създаване на ново оръжие да обхванат такъв период?
Грамадните гори на науката трябва да бъдат охранявани от дългоживеещи организации, способни да създават и поддържат дългоживеещи ценности, В миналото една такава организация беше църквата и макар, че сега тя до известна степен е лишена от миналото величие на времето, тъкмо с нейните усилия се създаваха университети, академии и други научни учреждения, които съществуват векове.
Тези дългоживеещи учреждения не могат да изискват надеждите и идеалите да бъдат превръщани незабавно в дребна разменна монета на днешния ден. Те съществуват благодарение на вярата, че усъвършенствуването на знанията е благо, което в края на краищатата трябва да принесе полза на цялото човечество.
Норберт Винер
Истинската наука започва от древна Елада. Математиката в Египет представлява полезни, но ограничени техники и методи за изчисление, измислени от писарите на държавна работа, във Вавилон са колекции от данни и методи за изчисление, от знания, но неорганизирани. Първата истинска система от знания е геометрията в Гърция – основана на логиката и логически непротиворечива теория, изградена подобно на къща –дефиниции за основи, аксиоми стъпващи на тях, теореми, изведени от аксиомите и доказателства за теоремите. Геометрията е избрана заради нейната непротиворечивост. Още по времето на Питагорейците, които измислят думата „математика“ от μάθημα (учение), се доказва, че съществуват т.нар. ирационални числа, които пречат на изграждането на логически непротиворечива аритметика – нещо, което и до ден-днешен остава нерешен проблем, ако не прибягваме до магията на трансфинитната индукция Weyl (2012). Идеята за изграждане на теорията върху логически непротиворечива основа е пренесена в Средновековието от Католическата църква и ислямските учени, за да бъде разширена и допълнена от емпирическия подход на учените от поколението на Галилей и след него. В древна Елада различните науки и изкуства не са били разделяни изкуствено. На въпроса на Леон, владетеля на Флиунт с какви науки и изкуства се занимава, Питагор отговорил[xi]:
„Аз не се занимавам нито с изкуства, нито с наука. Аз съм философ.“
Древногръцките академии (Фиг.5) са били място за интердисциплинарни проучвания, или биха били, ако там правеха това разделение. Мрежата от знание е била здраво свързана, което е позволило да се направи голям напредък за това антично време. След хиатуса, който Рим оставя в научното развитие, и който е ощетил тяхното технологично развитие много повече, отколкото практиката ги е научила (защото всичките им изобретения не натежават повече от откритията и изобретенията само на Архимед), през Средновековието в Европа църквата, а в халифата ислямските учени продължават делото. Манастирите, храмовете, джамиите и училищата към тях имат предимството на осигуреното финансиране и безкраен времеви хоризонт, без очакването на незабавни резултати в сфера, далеч от предсказуемото. Изследванията се допълвали от аристократи с осигурен доход и потомствено образование, ентусиасти с рано появил се гений и достатъчно късмет като Паскал или Гаус (който дълго време, след прославянето си бил беден) да имат благодетели или меценати. Развитието на съвременната наука в големи центрове като Франция, Германия и Русия е по волята и с помощта на техните владетели. В историята на Европа всички владетели, наречени „Велики“ са развивали образованието и научните изследвания – Карл Велики, Фридрих Велики, Симеон Велики, Петър Велики… Наполеон играе ключова роля във Франция и във възстановяването на финансирането на Ecole Polytechnique, орязано от френските революционери, защото „какво е това наука, яде ли се, пие ли се“. Това са същите, които убиват бащата на модерната химия Антоан Лавоазие въпреки молбата му да го оставят да си довърши изследванията с думите „твоята наука не ни трябва“[xii]. Значимостта на Лавоазие е резюмирана от Лагранж с думите Guerlac (1973):
„Отне им само миг да отсекат главата му и сто години могат да не стигнат, за да се появи подобна“
По думите на Наполеон „не се коли кокошката, която снася златни яйца“. Такова е и отношението на Фридрих Велики в Прусия и Петър Велики в Русия. Първият реорганизира хугенотската по произход Пруска академия на науките, като привлича именити учени. Вторият създава Руската академия на науките, като привлича много западни учени, между които Даниел Бернули и Леонард Ойлер (написал 90 тома математика) и от която тръгват руската математика, физика и инженерни науки. Академиите са места за чиста и приложна наука, като преподаването в началото е било на заден план и за ограничен кръг от хора. Естественото развитие през 19-ти век налага система от университети, организирани от държавата Витанов 2018, но академиите и институтите остават ключови за големите открития, макар и не в степента, в която са били през 17-ти и 18-ти век McNeely (2009).
Стремежът за прехвърляне на научните и технически изследвания изцяло в университетите и частния сектор противоречат на природата им, която в голяма степен не подлежи на планиране и прогнозиране в нито един от своите аспекти – нито „кой“, нито „как“, нито „кога“, нито „какво“. Управлението на такива рискови активи не се оптимизира чрез задаване на краткосрочни цели и третирането на учените като „научни работници“, сякаш работят на поточна линия. Потоците от информация са много по – сложно преплетени и са далеч от линейната подредба, която администраторите на научните системи си представят, които най-често не са учени, защото истината е, че учените днес не се самоуправляват. Отминало е времето на Платон и Аристотел, когато те са били основатели и господари на академиите си – сега те са наемни лица със статут на обикновени работници и третирани като такива, без да се отчитат разликите между вероятностните разпределения на представянето в обикновената и тяхната работа.
Когато в едно предприятие има разпределение на Парето и 20% от хората вършат 80% от работата, това е признак за лоша организация, защото талантът на хората е нормално (Гаусово) разпределен, освен ако то върши бизнес изцяло в областта на иновациите и откритията. Когато обаче в една академия или университет 20% от хората вършат 80% от работата, това е нормално и очаквано, но не означава, че другите 80% са маловажни. Трябва да се изгради цялостна научна култура, която да позволи на широката мрежа от взаимодействия да породи полюси, в които се фокусират резултатите – хора като Гаус, Нютон, Архимед, Еми Ньотер, Мария Кюри, Доналд Кнут, Луи Пастьор, Антоан Лавоазие. Тези полюси пренасят информация от цялата мрежа, те са продукт на средата и нейната организация. Добре организираната научна система се стреми да не пропуска неограниченото изкачване, което един човек може да ѝ донесе, което означава да простира мрежите си много нашироко и да има голям брой институти, академии, университети, държавни и частни лаборатории, както е в САЩ – Shapira and Youtie (2010). За държави, които не могат да внасят мигранти неограничено, това минава през образование, в пъти по – добро от средното за развития свят. Такова е положението в Сингапур, в който слабите ученици са едноцифрен процент, а държавата от 4 млн има 2 университета в топ 15 в света за 2018 г[xiii]. Нормалното разпределение на таланта означава, че екстремните прояви на опашката (гениите) са много силно зависими от средното ниво – малко покачване там увеличава броя на гениите многократно. Това е математическото основание за хвърлянето на широки мрежи върху цялото население в училище и върху много хора в университетите и академиите, вместо да се гони развиване само на вече проявените таланти, както е в България.

Фигура 5. Академията на Платон, мозайка от Помпей [xiv]
Мястото на научните институти в една широка мрежа от изследователски организации е да бъдат твърдите основи, които не се влияят от текущите тенденции, случайните колебания на пазара, популистките цели на краткосрочно избираните политически партии и лидери и всичко, което се мени с висока честота. В схемата за управление на рисковете, популяризирана от Насим Талеб като „метод на щангата“ Талеб (2014), институтите и академиите имат ролята на твърдата основа – техните изследвания се основават на академичната свобода, малко се влияят от външната среда и са устойчиви във времето. Университетите, фирмите и лабораториите се влияят по – силно от тенденциите, доколкото финансирането не е изцяло държавно, имат заложени по – краткосрочни цели и по – динамично интелектуално взаимодействие с пазара. Те са подложени на рискове от съкращения при обръщане на икономическите тенденции, но и по – бързо отговарят на краткосрочните нужди на пазара. Академиите и институтите от своя страна са място, където хората да задоволяват своето любопитство за чужда сметка без ограничения на целите – и така да не се изпуска неограниченото изкачване, което големият пробив носи.
За ползата от научните изследвания
Ползата от безполезното знание е в това, че тя е свойство на съвкупността Flexner (1939). Знанието е мрежа – ползата от един факт е ясна само чрез участието му в цялостната система на познани. Тя се подчинява отново на Парето или подобно на него разпределение – измеримите ползи се фокусират в малки полюси, които са проявления на цялата мрежа. Понякога трябва цяла академия, за да се отгледа една теорема, или едно изобретение.
Докато ползата от научните изследвания е безспорна, то ползата от търсенето на полза е съмнителна. Утилитаризмът побеждава сам себе си, тъй като интересите на днешния ден убиват ползите за утрешния. Гоненето на краткосрочни печалби е погубило много фирми, както разказва Деминг (2000), а търсенето на незабавни резултати от изследванията е довело до много фалшиви публикации с натъкмени данни Head et.al. (2015), тъй като за резултат се брои предимно потвърждаването, но не и отхвърлянето на хипотези. Стотици милиарди се дават всяка година по волята на първични когнитивни отклонения, което изкривява изследванията и ги отклонява от пътя с a priori неизмерими пропуснати ползи – когато печелиш, не знаеш какво губиш. Талеб (2013) отделя много време в дискусия по този въпрос, свързан с опитите да се планират откритията и техните неуспехи, в провала на телеологичния подход специално в медицината и в успеха на метода на щангата в науката, примери за което дава с английските викарии и тяхната роля в индустриалната революция. Това са хора с осигурен стабилен доход, независещ от годишна атестация. Те са с добро образование, богата библиотека и свободно време, движени от страст към експеримента и знанието – technê и Epistêmê[xv], двете сили, въртящи колелото на прогреса[xvi].
Каква е ползата от научните изследвания, освен, че извадиха милиарди от състоянието на крайна бедност, увеличиха продължителността на живота на жените до над тази на мъжете, направиха възможна прехраната на хората с лек труд, който не е опасен за живота, създадоха възможности за забавления и пътешествия отвъд всякакви мислими само преди век граници? Каква е ползата от знанието, от човешкия живот изобщо? Може би хората са средство за измерване на Вселената, според силния антропичен принцип, или просто случайност? И има ли полза от въпроси за ползата? Не е ли просто научното търсене част от търсенето на човека и човешкия род, търсенето на истината, на стойността, на значението? Не е ли то, което ги създава? Както Харди заключава в своята „Апология на математика“:
„Е, оправданието на моя живот, както и на живота на който и да е друг математик като мене е следното: аз съм добавил нещо към знанието и съм помогнал на други да добавят повече; че това има стойност, която се различава само по степен, но не и по вид от тази на творенията на великите математици или на който и да е от другите артисти – голям или малък – са оставили следа в паметта на човечеството.“
Източници
Айнщайн А., Борн М., Каприев Г. (прев.), Ланджев И.(прев.) 2018, Кореспонденция 1916-1955
Богданов Б. 1968. „Характерите“ на Теофраст – настояще и минало. Послеслов към Теофраст, Характери. НК, С. 1968, с. 66-77 (2 изд. Теофраст и неговите характери. Послеслов към Теофраст, Характери. НК, С. 1980, с. 131-143). http://bogdanbogdanov.net/pdf/108.pdf
Вайл, Х. 1969. Симетрия, Наука и Изкуство
Винер, Н. 1969. Аз съм математик, Народна Младеж
Витанов, Н.К. 2018, Черни и Бели Хроники на Николай К. Витанов, Българска Наука, http://image.nauka.bg/magazine/BG-Science-VITANOV.pdf
Деминг, У.Е. 2014. Изход от кризата, Рексинтегра
Конобеев Ю. и др. Стригачев А. (прев.), Стригачева Л. . (прев.), 1983. Физиците продължават да се шегуват, Наука и Изкуство
Клайн Ф., Долапчиев Б.(прев.), Чобанов И. (прев.), 1973. Развитие на науката през XIX-ти век, Наука и Изкуство
Талеб, Н. 2009. Черният Лебед, Инфодар
Талеб, Н. 2013. Антикрехкост, Инфодар
Томов, Л. Стажът като индикатор за успех, Българска наука, брой 104, стр.115-123 https://www.researchgate.net/publication/322131613_Stazt_kato_indikator_za_uspeh_Experience_as_a_mark_of_success
Харди, Г. 1971. Апология на математика, Наука и Изкуство
Biagioli, M. 2016. „Watch out for cheats in citation game“. Nature. 535 (7611): 201.
Booker, A.R. 2016. Turing and the Primes, In S. Cooper & A. Hodges (Eds.), The Once and Future Turing: Computing the World (pp. 34-52). Cambridge: Cambridge University Press
Euclid, Fitzpatrick, R (translator) 2007. Euclid’s Elements of Geometry, Lulu.com, http://farside.ph.utexas.edu/Books/Euclid/Elements.pdf
Edward, A.W. F. G. H. 2008. Hardy (1908) and Hardy–Weinberg Equilibrium, Genetics, July 1, 2008 vol. 179 no. 3 1143-1150
Flexner А. 1939. The Usefulnes of Useless Knowledge. Harpers, Issue 179, June/November 1939 https://library.ias.edu/files/UsefulnessHarpers.pdf
Galois, Évariste 1846. „Lettre de Galois à M. Auguste Chevalier“. Journal de Mathématiques Pures et Appliquées. XI: 408–415.
Goodhart, Charles 1981. „Problems of Monetary Management: The U.K. Experience“. Anthony S. Courakis (ed.), Inflation, Depression, and Economic Policy in the West. Rowman & Littlefield: 111–146.
Guerlac, H. 1973. Antoine-Laurent Lavoisier – Chemist and Revolutionary. New York: Charles Scribner’s Sons. pp 130.
Head ML, Holman L, Lanfear R, Kahn AT, Jennions MD 2015. The Extent and Consequences of P-Hacking in Science. PLoS Biol 13(3): e1002106
McCay-Peet L., and Wells, P.G. (2017) Serendipity in the Sciences – Exploring the Boundaries, Proceedings of the Nova Scotian Institute of Science, Volume 49, Part 1, pp.97-116
McNeely, I.F. 2009. The Renaissance academies between science and the humanities. Configurations. 17(3):227-58.
Shapira P., Youtie J. 2010. The Innovation System and Innovation Policy in the United States, Competing for Global Innovation Leadership: Innovation Systems and Policies in the USA, EU and Asia, Rainer Frietsch and Margot Schüller (Eds.), Fraunhofer IRB Verlag, Stuttgart, 2010, Chapter 2, pp. 5-29. http://www.euussciencetechnology.eu/assets/content/documents/InnovationSystemInnovationPolicyUS.pdf
Sinatra, R., Wang, D., Deville, P., Song, C. and Barab ́asi, A.-L. (2016). Quantifying the evolution of individual scientific impact, Science 354, 6312
Weyl, Hermann 2012. Levels of infinity: Selected writings on mathematics and philosophy. New York: Dover Publications.
[i] Релативистичната енергия зависи не само от масата в състояние на покой , наричана още инвариантна маса, но и от еквлидовата норма на различните моментни вектори
[ii] С безкраен брой измерения
[iii] Числото , определящо съотношението между дължината на окръжност и диаметъра ѝ е трансцедентално https://en.wikipedia.org/wiki/Pi
[iv] https://www.loc.gov/exhibits/vatican/math.html
[v] Алфред Норт Уайтхед, математик и философ, разработил заедно с Бертранд Ръсел йерархична теория на типовете, с която да заместят теория на множествата на Кантор и решат нейните парадокси
[vi] Прилича на обратното разпространение на грешката в невронни мрежи – това е процес, при който се пробват произволни експерименти и при наличие на резултати се прави разумна преоценка кои условия да се запазят при повторно експериментиране – една полу-случайна разходка с памет. Това е и подход, използван от Чарлз Дарвин, който заявявал, че отвреме-навреме трябва да се правят всякакви странни опити – ако нищо не се получи, не губим нищо, но ако има резултати, може да се получи голямо откритие.
[vii] английският термин за щастлива случайност, наричана от древните Фортуна
[viii] https://www.dartmouth.edu/~matc/MathDrama/reading/Wigner.html
[ix] https://www.quantamagazine.org/yitang-zhang-and-the-mystery-of-numbers-20150402/
[x] https://twitter.com/inspirehep/status/994589230146969601
[xi] Цицерон, Tusc. Disp. V, 3, 8-9.
[xii] Според апокрифната история съдията по делото казал: „La République n’a pas besoin de savants ni de chimistes; le cours de la justice ne peut être suspendu“ – Републиката не се нуждае от учени или химици; справедливостта не може да бъде отлагана.
[xiii] https://www.topuniversities.com/university-rankings/world-university-rankings/2018
[xiv] http://www.departments.bucknell.edu/History/Carnegie/plato/academy.html
[xv] https://plato.stanford.edu/entries/episteme-techne/
[xvi] По случайност съвпадащо с колелото на късмета






