Що е интелигентност
Коефициентът на интелигентност е създаден, за да измерва интелигентността, която се дефинира по следния начин:
“Умствено качество, което се състои от способността да се учиш от опита, да да се адаптираш към нови ситуации, да разбираш и да се справяш с абстрактни концепции и да използваш знанието, за да манипулираш околната среда”[i]
Съвременните дефиниции наблягат най-вече на адаптивността към околната среда, но такава адаптивност показват и хлебарките. Тук можем да се позовем на Уилям Едуардс Деминг, бащата на прилагането на статистическото управление на процеси в индустрията, услугите, здравеопазването и образованието (Деминг, 2014):
„Опитът сам по себе си не учи на нищо… Без теория опитът няма смисъл. Без теория нямаш въпроси, които да зададеш. Следователно, без теория няма учене“
Ученето от опита задължително изисква теория. Така са се развили всички науки, от математика и физика, през биология и химия, всички, които спазват критериите на Попър за опровержимост на твърденията – да се формулират теории, които имат само твърдения, подлежащи на проверка и евентуално отхвърляне. Такива твърдения трябва да заявяват необходими и достатъчни условия за настъпването на някакви явления или феномени, като условията на Маркс за световна революция. Това е позволило неговите идеи да бъдат подложени на тест и според Попър – да бъдат отхвърлени (Popper, 1945). Причината тези идеи на съветския марксизъм да останат в обращение е в липсата на ясен демаркационен критерий. Това според философията на Лакатош означава да е точно и ясно дефинирано какво трябва да се случи, за да се изостави дадена теория. Ако такъв липсва, тя може да се наглася според обстоятелствата, така, че да интерпретира по нов начин данните, за да продължи да обяснява със задна дата резултатите от проверката и да „бъде в съгласие“ с тях, но без да е способна да прави нови предказвания, които да спомагат за откриването на нови факти. Теория, която се променя, за да не могат твърденията ѝ да бъдат оборими и оттам оборени, но не създава нова информация и ново знание според Лакатош е мъртва. Една такава теория е адаптивна към околния свят, но не и антикрехка (Талеб, 2012) – тя не става по-силна от опроверженията, не расте нелинейно от атаките. Тя само се приспособява.
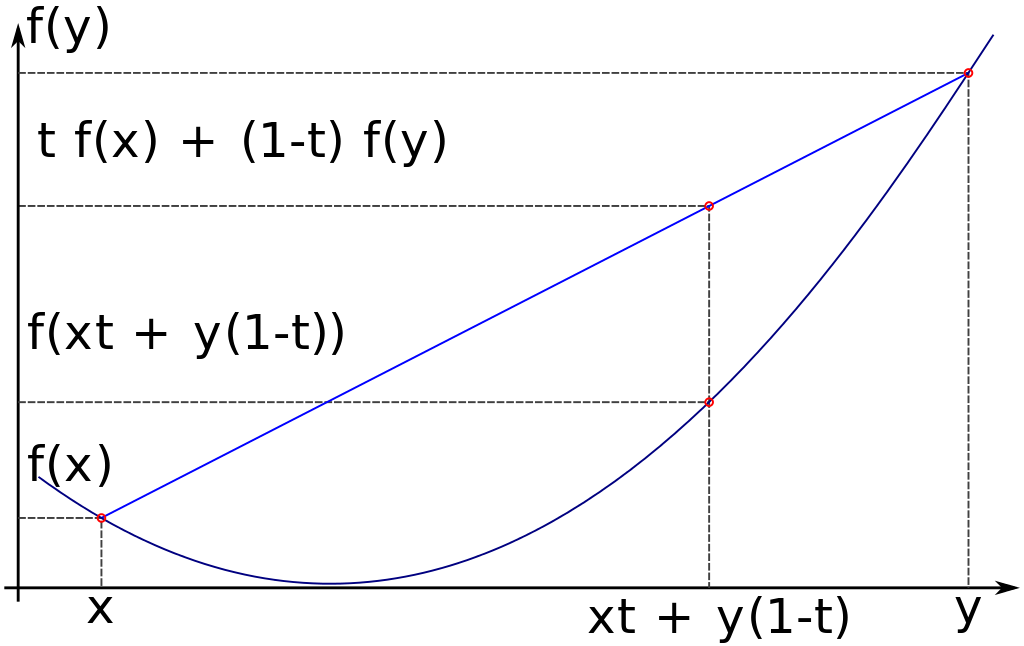
Фигура 1. Изпъкнала функция – претеглената стойност на функцията е по-голяма от функцията на претеглената стойност на аргумента. Правите свързващи всеки две точки на кривата на функцията са винаги над нея в този интервал на аргумента
Интелигентността е свързана със способността да се формира жива теория, тъй като това е единственият начин да се учиш. Евристичните правила, натрупани от опита имат ограничена валидност, докато теории като математическата и физическата имат универсална валидност. Правилата са информация, която е адитивна, докато теорията е знание, което е динамична, антикрехка система – изпъкнала спрямо случайните смущения, под формата на доказателства и опровержения – пример, за което дава (Лакатош, 1983) с формулата на Ойлер за многостените – множеството атаки по теорията водят до непрекъснати изменения в дефиниции и доказателства, което води и до общото доказателство на Поанкаре и решаването на цялостния проблем. Контрапримерите като смущения, водещи до непропорционално висока полза за теорията. Знанието е екосистема от теории, всички антикрехки до определено ниво (демаркационния критерий), но то самото е антикрехко, именно защото тяхната антикрехкост е ограничена – защото са опровержими. Опровержими са и самите методологии на научното изследване, като подхода на Аристотел за изцяло умозрително и основано на логиката изследване на природата, преборен от откритията на Галилей, Кеплер и Нютон. С това знанието бе драстично увеличено, също както биологичната световна екосистема става все по-силна след всяко катастрофално събитие – и колкото по-катастрофално е то, толкова по-добре се развива тя. Теориите са по необходимост абстрактни доколкото абстракцията е еволюционна необходимост – тъй като минимизира необходимата енергия за съхранение на информацията в мозъка. Успехите на абстрактните теории са толкова чудодейни и в разрез със законите на вероятностите, че стават повод нобеловия лауреат по физика Юджийн Уигнър (един от т.нар. „марсианци“- група унгарски математици и физици с невероятно постижения), който въвежда употребата на абстрактната и красива теория на групите във физиката да напише специална статия „Удивителната ефективност на математиката в природните науки“ (Wigner 1973: 98):
„Светът около нас е объркващо сложен и най-очебийният факт за него е, че можем да предвиждаме бъдещето. Макар известната шега да приписва на оптимиста възгледа, че бъдещето е несигурно, в този случай оптимистът е прав: бъдещето е непредсказуемо. Както отбелязва Шрьодингер, цяло чудо е, че въпреки загадъчната сложност на света в явленията могат да се открият известни закономерности. Една такава закономерност, открита от Галилей, е, че два камъка, пуснати по едно и също време от една и съща височина, стигат до Земята за едно и също време. Законите на природата са свързани с такива закономерности. Закономерността на Галилей е прообраз на широк клас закономерности. Тя е изненадваща закономерност поради три причини.
Първата причина за нейната неочакваност е, че е вярна не само в Пиза, но и по времето на Галилей, но че е вярна навсякъде по Земята, била е винаги вярна и пак ще бъде вярна. Това свойство на закономерността е осъзнато инвариантно свойство и преди известно време аз имах възможност да посоча, че без принципи на инвариантност, подобни на този, който следва от това обобщение на наблюдението на Галилей, не би била възможна никаква физика. Втората неочаквана особеност е, че разглежданата закономерност не зависи от толкова многото условия, които биха могли да влияят върху нея. Тя е в сила независимо от това, дали вали или не, дали опитът се провежда в стая, или от наклонената кула, независимо от това дали лицето, което пуска камъка е мъж или жена… Очевидно има безброй други условия, които са несъществени от гледна точка на валидността на закона на Галилей. Неподатливостта на толкова много обстоятелства, които биха могли да играят роля в наблюдаваното явление също е наричана инвариантност…. И тъй, вярно е твърдението, че ако нямаше явления, които да са независими от всички освен от едно управляемо малко множество от условия, физиката би била невъзможна.
… Предишното разглеждане има за цел на първо място да припомни, че съществуването на „природни закони“ съвсем не е естествено, а още по-малко естествена е възможността човек да може да ги открива (Е. Шрьодингер в книгата си What is Life, Camebridge, 1945, стр.31 пише, че това второ чудо може би надхвърля човешките възможности за разбиране)“
Знанието може да има подобна антикрехкост, като описаната от Уигнър само в условията на един познаваем свят и на боравенето с абстрактни понятия и с помощта на теории. Евристичните правила и традициите просто не са достатъчни, защото те са адитивни, а не са изпъкнали – добавянето на евристични правила увеличава само информацията, която е линейна функция на вероятностите на независимите събития, а не теориите, което създават нова информация и са мултипликативни и изпъкнали. Колекцията от правила, като използваните от римските строители не е довела до създаването на напълно нови машини и методи, единствено са усъвършенствувани старите. Всичко ново, създадено от римляните е плод на инцидента, наричан от Марк Твен „най-великият изобретател“. Подобни изобретения обаче се натрупват линейно – не се извлича знание от инцидентите, за да се предскаже нещо напълно ново, така както например теориите на Айнщайн предсказват появата на черните дупки и правят възможни геостационарните сателити, или откритията на модерната физика, правещи възможни новите квантови алгоритми които могат да разбият традиционните криптиращи защити.
Що е IQ и как се измерва
Интелигентността е свойство на живите същества да създават живи теории (доколкото това могат да правят други видове освен човека), за да увеличават силата и обхвата на видовата антикрехкост, поради което и включва създаването и оборването на теории – разпознаването и отхвърлянето на модели, за което са специално разработени тестовете като тези на Менса. Резултатите от тези изследвания имат политически и социокултурни импликации поради намерените разлики между различните държави и континенти (Фиг.2)
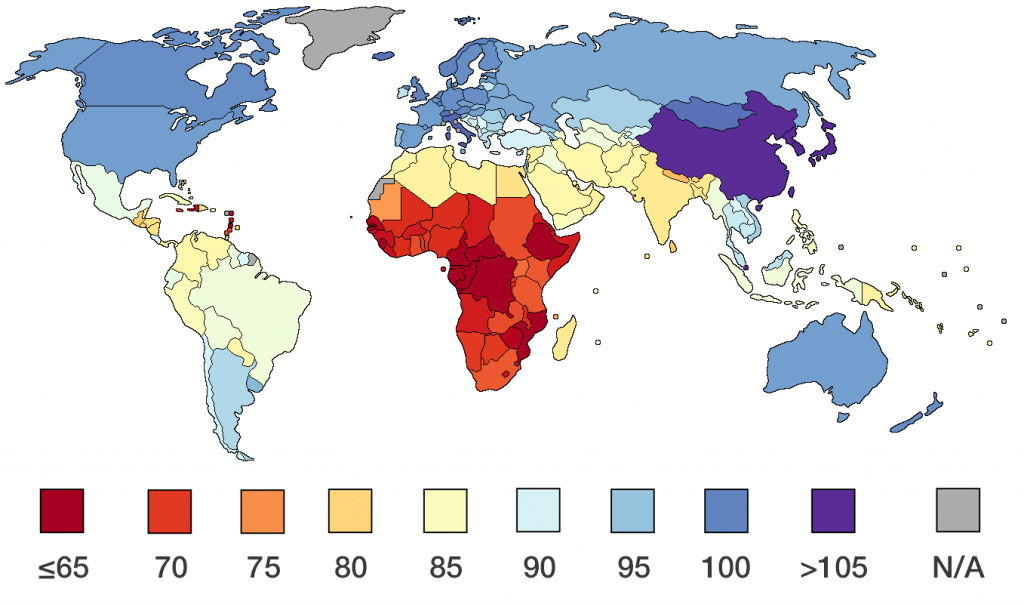
Фигура 2. Разпределение на IQ по географски региони, според (Lynn and Vanhanen, 2006), показващо значими концентрации – зони с високо и ниско IQ с големи разлики между Източна Азия и суб-сахарска Африка
В предишна статия, озаглавена “За интелигентността, религиозността и прибързаните изводи”[ii] разгледахме този проблем задълбочено и обърнахме внимание как подобно териториално разпределение може да се тълкува по много начини (географска, културна, биологична или политическа картина е това?), да е продукт до голяма степен на образованието и дори да е плод на случайност, а не състояние, което да се екстраполира хилядолетия назад. В този аспект употребата на тези данни за „расови“ заключения е спекулативна и неоснователна. В този план, възраженията на Насим Талеб срещу употребата на този коефициент на интелигентност имат своите основанията.
За измерването на общата интелигентност съществуват множество тестове, които се опитват да оценят неща като тест на Уечслър[iii], Станфорд-Бине други, създадени, за да измерват редица елементи на когнитивните способности като скорост на обработка, работна памет, вербално разбиране, абстрактно разсъждение (геометрична интуиция и извличане на модели чрез нея). Тестовете като тези на организацията Менса са от вида, показан на Фиг.3. Задачите изискват извличането на модел и предсказването на следващата картинка по него, класическа проява интелигентност, чиято кулминация е в математиката и физиката. Нещо повече – тъй като съществуват безкрайно множество модели, които се описват с краен брой данни, то това е задача и по отхвърляне на излишно сложни зависимости, или следване на прословутия „Бръснач на Окам“. Проявата на интелигентност е свързана не просто с избирането на модел, а и на такъв, който е най-правдоподобен, което често (но не винаги) съвпада и с най-простия модел. Такъв е и законът за всемирното привличане на Исак Нютон, който използва безразмерни масови точки, а не тела и проста формула (произведение на масите, разделено на квадрата на разстоянието), която улавя удивително точно гравитационното взаимодействие. Нютоновата механика позволява откриването на планети като Нептун по чисто теоретичен път, преди тя да бъде наблюдавана, като най-правдоподобното обяснение на определени ирегулярности в орбитата на Уран. Тестовете за интелигентност измерват определено умение да се отсеят зависимостите според тяхното правдоподобие, а не само наивното разпознаване на модели с произволна сложност, обратно на това, което Насим Талеб твърди[iv].
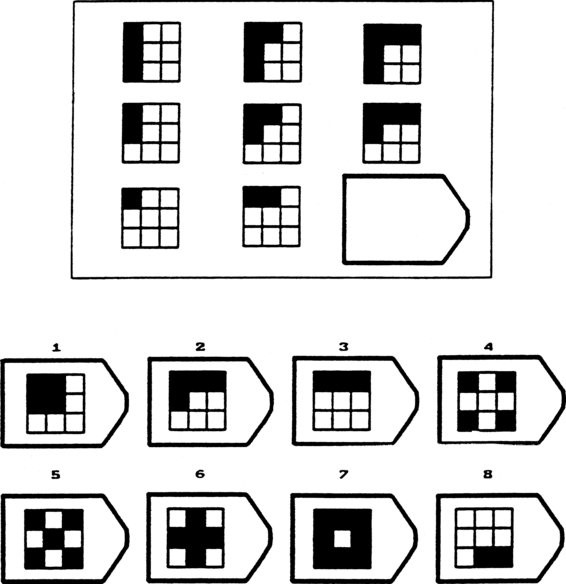
Фигура 3. Типичен тест от вида „Прогресивни матрици на Рейвън“[v]
Безкритичното приемане на всякакви сложни модели е характерно за конспиративното мислене, което не е положително асоциирано с коефициента на интелигентност. Хората не са добре екипирани, да разпознават пълната липса на модел (случайността), но в рамките на наличието на някаква зависимост тези тестове измерват способността да се подбира най-правдоподобният модел. Терминът „правдоподобие“ тук използваме вместо „вероятност“ в съгласие с евристичния модел на Дьорд Поѝа[vi] (Поѝа, 1976), което е по-подходящо за описание на избора, който хората правят, когато проявяват интелигентност.
Необходимо условие, за да бъде тестът за IQ смислен, е да съществува уникално оптимално решение на задачите, подобни на тези от Фиг.3,. Възможните модели са безброй, но най-простият модел трябва да е само един и до него не трябва да се приближават чувствително други решения. По-простите модели изискват по-малко независими предположения и описват инутитивно по-добре наблюдавания процес. Лоши задачи са подобни на тази:
Да се продължи редицата: „3,5,7…“
Тук и трите числа са нечетни, но са също така и прости, еднакво правдоподобно е да се добави 9, както и 11 като следващо число. Отговорът тук няма помогне да се измери интелигентност.
В други ситуации задачите имат различни решения, само едно от които обаче е оптимално:
3,6=27
5,8=39
1,7=48
3,4=?
Лесно е да се забележи, че 3+6=9 и 3*9=27 на първия ред, а на втория 5+8=13 и 3*13=39, т.е. за първите два реда има общ закон – сумата на числата се утроява. За третия ред обаче, сумата на числата 1+7=8 се умножава по 6, което е два пъти по-голямо число. Тук, за да се запази първоначалното хрумване трябва да се предположи ново правило, при което умножаването се променя, но как – на всеки два реда, на всеки трети ред, всеки път се удвоява предишното? Това е пътят на параноика, не на интелигентния човек, тук разумът не е обуздан и броят параметри на модела непрекъснато нараства. Данните не се използват пълноценно и за сметка на тях расте сложността на модела.
Човек, който търси от простото към сложното, може да види нещо друго – разликата между 6 и 3 е 3, а между 8 и 5 отново е 3 и това е именно коефициентът на умножение. Проверката с 1 и 7 потвърждава това правило, вместо да го усложнява, следователно то е валидното – 7-1 = 6.
Правилото може да се запише като (b+a)*(b-a) за двойката числа a,b – произведение на сумата и разликата на двете числа, което отразява и факта, че винаги второто е по-голямо от първото – още една данна, използвана в този модел, вместо да му се добавя параметър, или да се усложни.
Добре поставените задачи изискват много повече отхвърляне, отколкото приемане, тъй като множеството на потенциалните кандидати е безкрайно. Отхвърлянето на един модел за сметка на друг, по-прост е триумф именно на абстрактното мислене. Неговият провал е неспособността да се отхвърли моделируемостта на данните. – да се отрече случайното, когато никой краен закон или модел не биха ги обяснили добре.
Коефициентът за интелигентност е показател, който съществува, т.е. поне от гледна точка на статистиката, тъй като неговите стойности при измерване на големи и представителни групи от хора се апроксимира отлично от нормалното разпределение (Фиг.4)
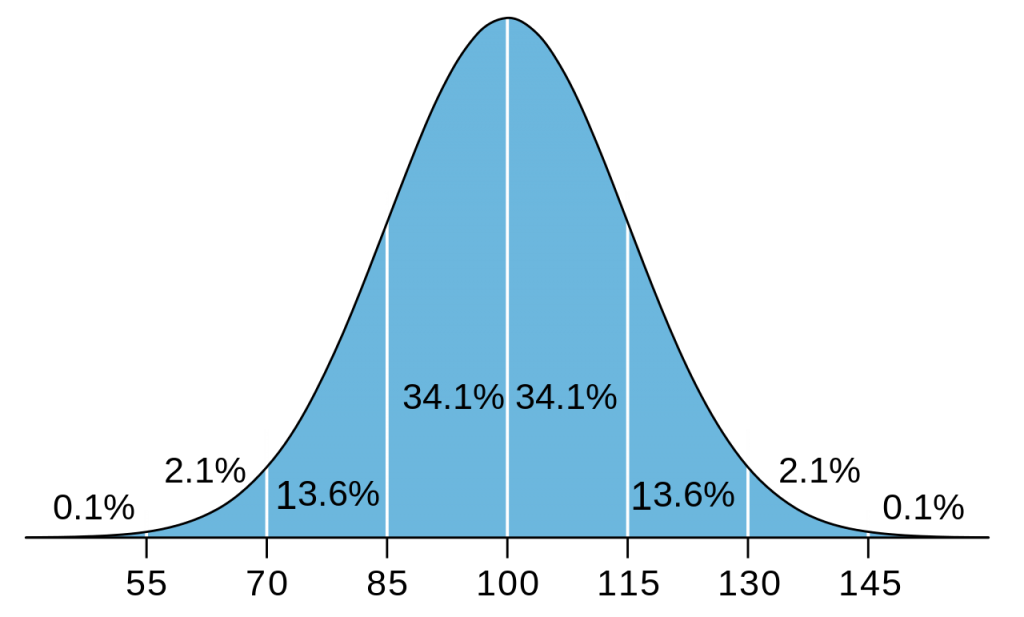
Фигура 4. Нормалното разпределение на плътността на вероятността за стандартизирания IQ тест. Т.нар. гениално ниво се определя от стойностите, надвиващаши три стандартни отклонения или най-високите 2%
Това е разпределение с тънка опашка, което неформално означава, че вероятността за екстремен резултат намалява много бързо – само 0.1% от хората имат над 145 точки при среден резултат от 100. Това е разпределение, което не максимизира ентропията на Шенън, за разлика от равномерното, което така носи най-малко информация (Conrad 2019) и при което показателят не би имал същото значение, тъй като при него всеки резултат би бил равновероятен. Наличието на нормално разпределение увеличава правдоподобността на твърдението, че тестът измерва нещо обективно, подобно измерванията на движенията на планетите в астрономията – някакъв биологичен закон. Също както измерванията в астрономията с техните нормални разпределения показват закономерност и грешка от измерване, тук е по-правдоподобно също да има подобна закономерност и тестът да има смисъл.
Важно уточнение е, че това е статистически инструмент, който има грешка в оценяването и измерва най-точно стойностите, които са най-близо до средната. Човек, който има 100 точки, може да вземе няколко теста и резултатите му ще варират, но в приемливи рамки, например 97-102. Стандартната грешка от измерване[vii] нараства с отдалечаване от средната стойност и е най-висока в двата края на разпределението, т.нар. опашки, като е толкова по-голяма, колкото по-голямо е стандартното отклонение на самия тест ( при IQ обикновено е 15 точки) и колкото по-малка е надеждността на теста. Тестове с надеждност от 90% могат да произведат ситуация, в която при медицински изпит от 1565 кандидати минали първия изпит с 60% и повече едва 1107 взимат и втория изпит поради стандартната грешка от измерване (Tighe et.al. 2010). Грешката при измерване на истинското IQ дава 95% доверителен интервал от общо 40 точки – 10 под измерената стойност и 18 над нея (Whitaker 2010). Различните измервания ще попаднат с 95% вероятност в този интервал от поне 28 точки около истинската стойност на коефициента. Това обяснява феномена „Ричард Файнман“ – гениален учен, получил „само“ 127 точки на тест като млад – едно повтаряне на теста би могло да промени резултата много по-чувствително при него, отколкото при някой човек със средна интелигентност. Това възражение и на него и на Талеб към тестовете не е по същество – тестът не се е провалил да измери интелигентността на физика. Процедурата за тестване трябва да включва повече измервания, за да компенсира за стандартната грешка от измерване.
Основните възражения срещу IQ
Възраженията срещу IQ като адекватен измерител на интелигентността не са нови, но на тях бе даден нов глас с пост на популярния статистик и трейдър Насим Талеб. Основно те са две групи – възражения срещу дефиницията за интелигентност и възражения срещу IQ като измерител на сложни процеси, от което обаче се правят некоректни изводи.
Първото възражение на Насим Талеб е, че интелигентността не е това, което се измерва от този тест. На това възражение отговорихме в предишните части на изложението и по същество представлява игра с дефиницията. Тривиално е да подмениш дефиницията за интелигентност с „хитрост“, „оправност“ или „способност за оцеляване“, първите две от които имат дори и някои висши примати, а последното е най-добре развито у бактериите. Тогава инструментът, който мери абстрактното мислене и способността за трупане на знание чрез създаване на смислени теории, просто няма да отговаря на тази нова дефиниция, следователнот той е безсмислен. Това е евтин трик. Способността да се конструират смислени теории чрез боравене с абстрактни концепции сама по себе си е плод на еволюцията и на един оптимизационен процес, който разяснихме по-рано. Това е свързано и с писмеността, с езика и и със способността да се учиш от опита по нетривиален начин, позволяващ предсказване, за което е необходима теория. Както и самият Талеб казва, винаги трябва да търсим мотивите зад всяко изказване – и това в случая е неговият уклон в полза на традицията и евристиката, въпреки, че самият той ползва математиката нашироко, за да докаже ползата от тях. Неговото възхищение към римляните с техните евристични методи за строежи на акведукти и мостове под формата на рецепти удобно игнорира как Ератостен е измерил с висока точност радиуса на Земята с геометрия или как е построен тунелът на остров Самос, строен едновременно от двете страни на варовиковата планина Кастро (Ван дер Варден, 1968). Гръцкият инженер Евпалин изчислява с помощта на геометрия (Фиг.5) толкова точно как да се копае този тунел, че при дължина от общо един километър, разминаванията при срещането на двете групи е 10 метра в хоризонтално и 3 метра във вертикално направление, под 1% грешка!
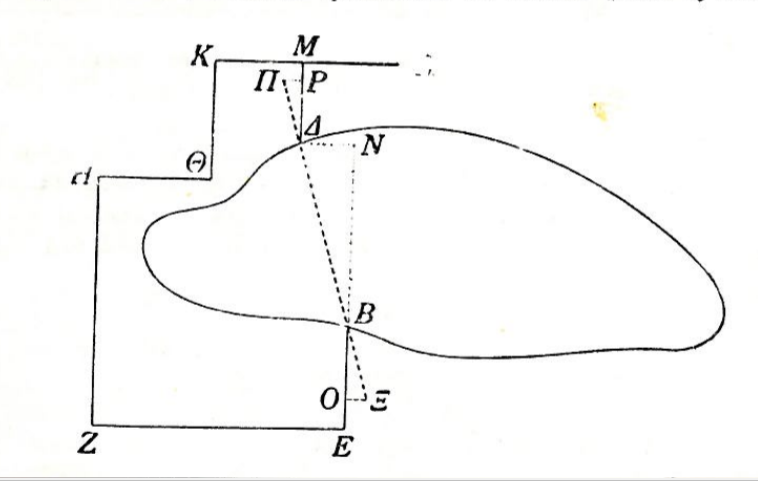
Фигура 5. Изчисленията на Евпалин с помощта на механичния инструмент „диоптър“, описано от Херон Александрийски (възстановка на Шьоне) . Съвременните анализи дават по-сложен геометричен метод и по-висока актуална точност на строежа – само няколко дециметра разминаване във височината[viii]
Шансът може да бъде системно двигател на научния прогрес само в присъствието на теория, която да се възползва нелинейно от него – характеристиката, която традициите и правилата не притежават, тъй като са несистемни. Знанието само по себе си е сложна система и този, който често с право обвинява колегите си учени, че не разбират системите, също е жертва на това неразбиране.
Втората група от аргументи на Талеб е срещу IQ като статистически измерител и отново показва неразбиране на сложните системи. Основното твърдение е, че коефициентът показва слаба корелация с различни системни характеристики като богатство, справяне на работа и други. Корелацията е най-силна при ниски стойности и отслабва при по-високите нива на IQ (Фиг. 6) Тълкуването на Талеб е, че IQ може да мери само екстремна липса на интелигентност, но не и високата такава. Донякъде той има право с оглед на това, че измерването в опашките на разпределението е много по-несигурно от това в центъра, което описахме в предишна част на статията. Това лесно може да се коригира с по-надеждни тестове и няколко измервания на човек (поне две независими такива).
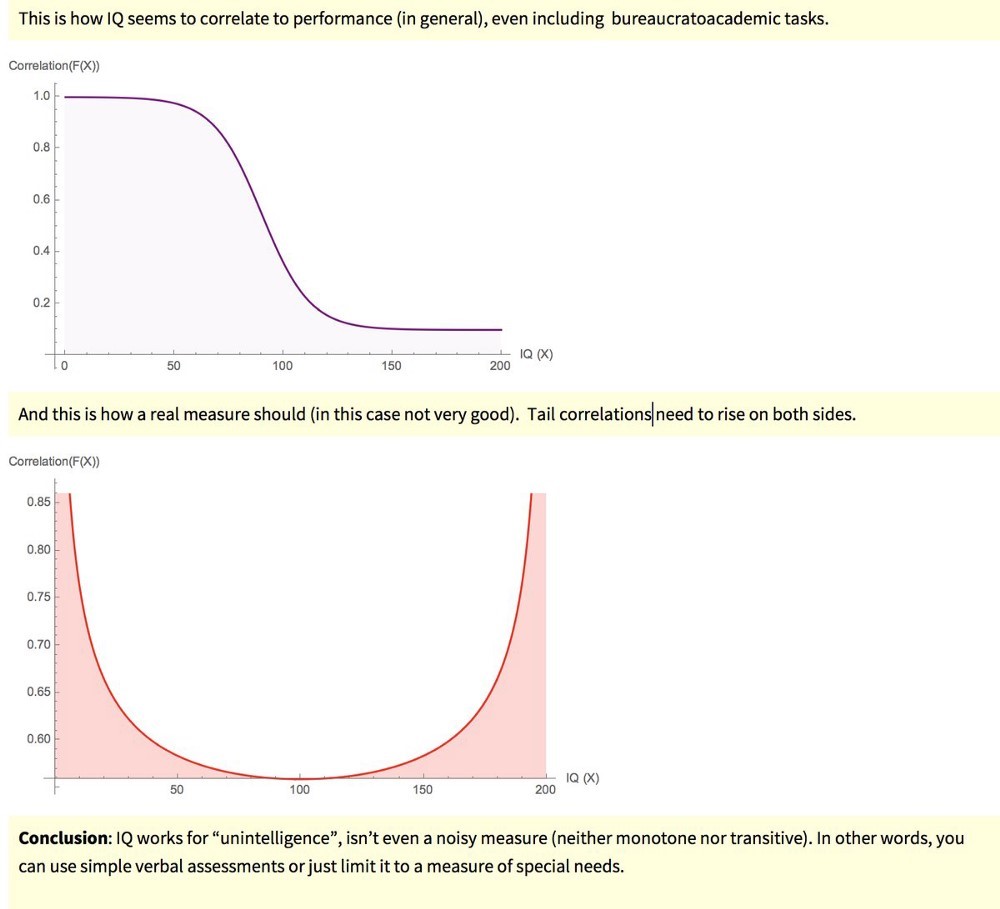
Фигура 6. Корелацията на IQ според Талеб и как би трябвало да изглежда с представянето на работа (пак според него)
Талеб пропуска в случая, че IQ измерва индивидуални способности, а представянето на работа – не. Справянето на работното място е 90% продукт на организацията според данните и опита на Деминг и изследванията като Google Aristotle Project го потвърждават. Няма корелация с индивидуални характеристики, като опит, образование и дори IQ, корелация има с организацията на различните екипи и особено как те общуват помежду си[ix]. Липсата на корелация с индивидуалните способности е потвърдена и от изследванията за колективната интелигентност – при нея няма корелация с индивидуалната, нито с максималната такава (Wolley et.al. 2010). Това е старо българско знание, плод на хилядолетна традиция и мъдрост, евристичното правило „ум царува, ум робува, ум патки пасе“, т.е. няма корелация между ума и справянето и дори избора на работа. Талеб отбелязва, че най-умните 25% от чистачите според статистиката са по-умни от най-глупавите 25% от учените, което е резултат именно на това и според него това обезсмисля IQ като инструмент или, че той не измерва наистина интелигентността.
Това се нарича „да бъркаш липсата на доказателство за доказателство на липса“. Тук няма да спорим около самите му статистически твърдения, въпреки наличието на голям обем от изследвания, а ще се фокусираме върху изводите от представените доказателства.
Първо – твърдението, че истинският измерител на интелигентността трябва да е силно корелиран в опашките е по същество невярно, не и както е приложено. Нищо не може да се корелира индивидуално с поведението на една сложна система. Представянето на работа, избора на работа и богатството не са интелигентността, а са процеси, зависещи евентуално от нея.
Второ – липсата на корелация на един показател не означава липса на зависимост. Основна истина от статистиката е, че различни взаимно независими променливи може поотделно да не показват корелация със зависимата променлива, но тяхна линейна комбинация да обяснява много силно нейното поведение и да има висока статистическа значимост – сумата е по-голяма от частите си. Пълната липса на корелация означава единствено, че не е намерена засега линейна зависимост.. Всяка една нелинейна зависимост[x] няма да покаже корелация.
Трето – формата на тази корелация от Фиг.6 показва именно поведение на нелинейна система – има насищане от ползата от индивидуалнaта интелигентност при представянето на работа. Това е подобно на подобряването на бързодействието на паралелната обработка на информацията при добавянето на нови процесори – зависи от процента от работата, която може да се паралелизира, т.нар. Закон на Амдал (Фиг.7)
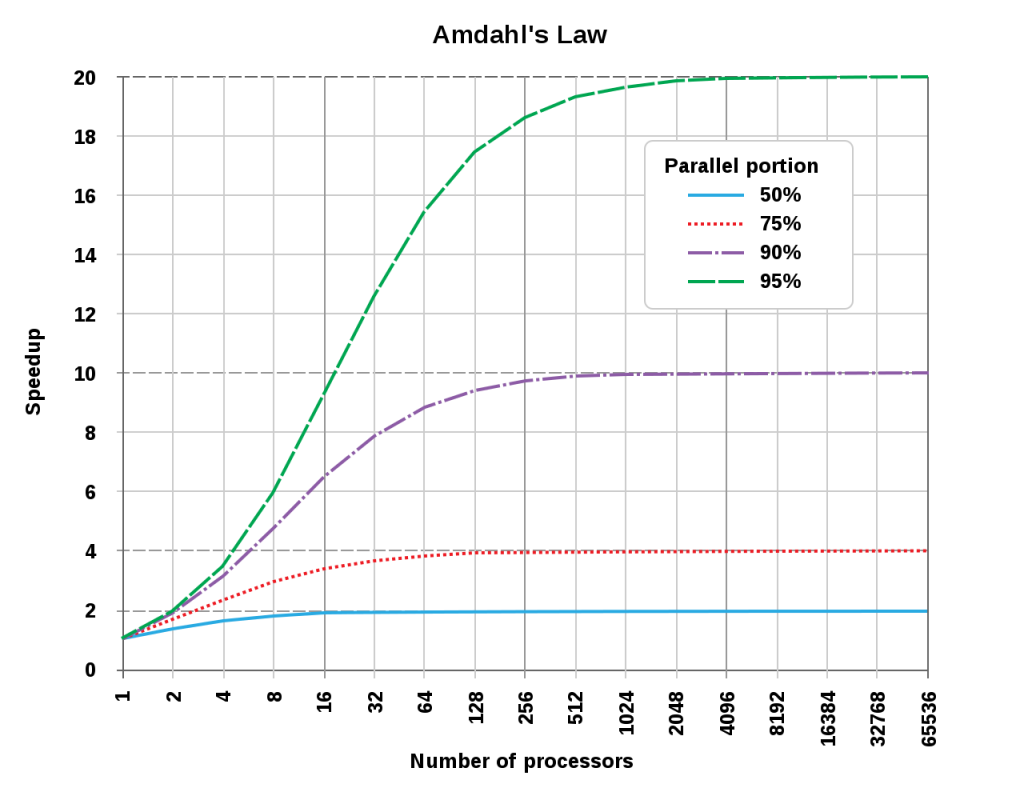
Фигура 7. Закон на Амдал – ползата от добавянето на нови процесори има апериодичен характер и е ограничена от процента от работата, който може да се паралелизира[xi]
Същото важи и за работата в компания – серийната зависимост между работниците създава бариери за използването на интелигентността на кадрите над определено ниво, като това се дължи изцяло на организационни, системни причини ина управлението. Това обяснение не е по-лошо от обяснението, че IQ изобщо не измерва интелигентността и, че е лош измерител. То изглежда и по-правдоподобно в светлината на изследванията като това на Гугъл, които не откриват корелация с нито един индивидуален фактор.
Обратният проблем
Съществува един състоятелен аргумент срещу безкритичното приемане на всички статистически изследвания и заместването на измерваното с неговия измерител и това е т.нар. „обратен проблем“, описан в нашата статияii. Обратният проблем е като пример задачата по проекцията на една триизмерна фигура в равнината да се възстанови фигурата – той има безброй много решения. Проблемът за отсяване на най-правдоподобните решения от безкрайното им множество е свързан с интелигентността, както описахме тук, но той е и свързан с ограниченията на всеки един тест за интелигентност, колкото и да се развива и подобрява с времето – измерваното не се представя напълно от измереното. Прост пример е връзката между IQ и уменията в шаха, където корелацията е по-силна сред по-малко опитните играчи, т.е. където се използва интуицията (Burgoyne et.al 2016). Дори нещо толкова математизирано като играта на шах включва по-комплексен набор от променливи освен интелигентността и нейната проекция IQ, свързани с опита и стажа. От интелигентността не по-маловажно е Времето, този велик учител. Означава ли, че IQ е без значение, или, че измерва много малка част от самата интелигентност? Не и ако приемем, че уменията за съставяне на най-правдоподобни модели, т.е. теоретизирането е ядро на общите когнитивни умения и се намира във всяка тяхна проява. Това не би показало сериозни стойности на корелацията, по същия начин, по който между височината на играчите и отбелязаните точки в баскетбола корелация няма (Burgoyne et.al. 2015), но е тя не е никак маловажен фактор за победата и е ядро – участвува във всеки компонент на играта – в защита, подавания, в точността на стрелбата. Това са поуки от опита и традицията, чакащи добра теоретична формулировка и обосновка, която да произведе ново знание.
Заключение
В едно отношение Насим Талеб има право – не можем с лека ръка да приемаме всяко статистическо изследване, което свързва IQ с една или друга характеристика, нито да смятаме, че най-сложната система в природата, която е човешкият мозък е достатъчно изучена, за да сме сигурни, че подобни метрики описват пълната картина на човешката интелигентност. Със сигурност използването за расови, политически или религиозни аргументи е крайно съмнително. Също така IQ не показва големи корелации с много от сложните процеси, в които ние, хората участвуваме, но това е по-скоро от тяхната природа, отколкото от неговата. Това означава ли, че той не измерва интелигентността въобще? Такъв извод би бил ненаучен и неинтелигентен, както и всеки опит тя да се обоснове кръгово, като „способност за оцеляване“ – оцеляването е на най-приспособените, а по дефиниция най-приспособените са тези, които оцеляват. Талеб обвинява дефиницията за интелигентност в кръговост, но прилага същия подход в неговия вариант. Той всъщност така отрича ролята на шанса в оцеляването и преувеличава същия този шанс в еволюцията на знанието. Шансът е двигател на антикрехката система, ядро на която са теорията и абстрактното мислене, а не единственият производител на информация.
Образованият скептик, казва Файнман, борави с вероятности. Тестовете за интелигентност вероятно не измерват всичко, на което мозъкът е способен, но още по-вероятно е да измерват неща, които имат значение за творческата човешка дейност – нещо, с което се отличаваме като вид от всички други, а не толкова по способността си за оцеляване във всякакви условия (целта и пътят не са едно и също нещо). Основателните съмнения срещу прилагането на тестовете за интелигентност почиват на основателни аргументи, които изключват подмяната на дефинициите, кръговите логики, уклона към определени теории на познанието и заместването на липсата на доказателства с доказателства за липса. Такива има изброени както от Талеб, така и от нас.
Литература:
Ван дер Варден (1968). Пробуждаща се наука, Наука и Изкуство
Деминг, У.Е. (2014). Изход от кризата, Рексинтегра
Лакатош, И. (1983). Доказателства и опровержения, Наука и Изкуство
Поѝа, Д. (1976). Математиката и правдоподобните разсъждения: Том Втори. Схеми на правдоподобни заключения, Наука и Изкуство
Талеб, Н.Н. (2012). Антикрехкост – как да извлечем ползи от хаоса, Инфодар
Alexander P. Burgoyne, Giovanni Sala, Fernand Gobet, Brooke N. Macnamara, Guillermo Campitelli, David Z. Hambrick. The relationship between cognitive ability and chess skill: A comprehensive meta-analysis. Intelligence, 2016; DOI: 10.1016/j.intell.2016.08.002
Carter, Tom (March 2014). An introduction to information theory and entropy (PDF). Santa Fe. Retrieved 4 August 2017.
Conrad, Keith. (2019). Probability Distribution and Maximum Entropy, https://kconrad.math.uconn.edu/blurbs/analysis/entropypost.pdf.
R. Lynn, and T. Vanhanen. (2006). IQ and global inequality. Athens (2006).GA: Washington Summit Publishers.
Popper, Karl. (1945).The Open Society and lts Enemies, Vol.II. London: Routledge and Kegan Paul
Tighe, J., McManus, I. C., Dewhurst, N. G., Chis, L., & Mucklow, J. (2010). The standard error of measurement is a more appropriate measure of quality for postgraduate medical assessments than is reliability: an analysis of MRCP(UK) examinations. BMC medical education, 10, 40. doi:10.1186/1472-6920-10-40 https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2893515/
Torres-Unda, Jon & Zarrazquin, Idoia & Gravina, Leyre & Zubero, Jaime & Seco, Jesús & Gil, Susana & Gil, Javier & Irazusta, Jon. (2015). Basketball Performance Is Related to Maturity and Relative Age in Elite Adolescent Players. Journal of strength and conditioning research / National Strength & Conditioning Association. 30. 10.1519/JSC.0000000000001224.
Whitaker, S. (2010). Error in the estimation of intellectual ability in the low range using the WISC-IV and WAIS-III. Personality and Individual Differences, 48(5), 517-521.
Anita Williams Woolley, Christopher F. Chabris, Alex
Pentland, Nada Hashmi, Thomas W. Malone (2010), Evidence for a Collective
Intelligence Factor in the Performance of Human Groups Science29 Oct 2010 :
686-688
[i] https://www.britannica.com/science/human-intelligence-psychology
[ii] https://conservative.bg/za-inteligentnostta-religioznostta-i-pribarzanite-izvodi/
[iii] https://images.pearsonclinical.com/images/assets/WAIS-IV/WAISIV2_6_08.pdf
[iv] https://medium.com/incerto/iq-is-largely-a-pseudoscientific-swindle-f131c101ba39
[v]https://www.researchgate.net/publication/307465310_On_Mathematical_Reasoning_-_being_told_or_finding_out/figures
[vi] https://drive.google.com/file/d/1oAdhxDh-p1YH0bSeytc1cNftZD7amjEc/view?usp=sharing
[vii] https://www.statisticshowto.datasciencecentral.com/standard-error-of-measurement/
[viii] https://en.wikipedia.org/wiki/Tunnel_of_Eupalinos
[ix]https://www.nytimes.com/2016/02/28/magazine/what-google-learned-from-its-quest-to-build-the-perfect-team.html
[x] https://stats.stackexchange.com/questions/85363/simple-examples-of-uncorrelated-but-not-independent-x-and-y
[xi] https://en.wikipedia.org/wiki/Parallel_computing#/media/File:AmdahlsLaw.svg






